Método de Bisección
Mediante FMSLogo y la biblioteca LogoFE (para las gráficas).
Contenido
2. Descripción de Método de Bisección
3. Adaptación Gráfica
4. Mayor Precisión
5. Aplicaciones
6. Licencia
7. Preguntas, Dudas, Comentarios, Peticiones
8. Enlaces
1. Trabajando con funciones
FMSLogo puede evaluar funciones primitivas, de la biblioteca, o definidas por el programador con el función invoca. Por ejemplo en la línea de comandos de FMSLogo podemos escribir:
haz "f leepalabra
sen
escribe :f
sen
escribe invoca :f 45
0.707106781186547
la variable f tiene como valor la palabra sen leida desde el teclado, sen es una función primitiva (es parte del lenguaje) que trabaja en grados
para doble :n
devuelve 2 * :n
fin
haz "f "doble
escribe invoca :f 45
90
la variable f tiene como valor la palabra doble que es una función definida desde la línea de comandos
haz "f [[x] 2 * sen :x]
escribe invoca :f 45
1.41421356237309
escribe invoca [[z] 2 * sen :z] 45
1.41421356237309
la variable f tiene como valor una lista equivalente a la función matemática: f(x) = 2 · sen(x)
2. Descripción de Método de Bisección
Trabajemos con la ecuación:
cos(x) = 0.01 · x
Esta ecuación no puede resolverse por métodos algebráicos. Es necesario utilizar métodos númericos para encontrar un valor de x que satisfaga la ecuación. Uno de estos métodos es el método de bisección. El método busca el valor de x para el que una función continua devuelve cero. Por lo que definamos la función, a partir de la ecuación anterior, de la siguiente manera:
f(x) = 0.01 · x - cos(x)
Si encontramos un valor de x adecuado para el que la función f es cero, podremos plantear:
0 = 0.01 · x - cos(x)
cos(x) = 0.01 · x
Y consecuentemente, la ecuación se cumplirá.
El método necesita un intervalo tal que, para un extremo del intervalo, el valor de la función sea nagativo y para el otro extremo del intervalo, el valor de la función sea positivo. Veamos si esto se cumple para el intervalo (-200,200):
escribe invoca [[x] 0.01 * :x - cos :x] -200
-1.06030737921409
escribe invoca [[x] 0.01 * :x - cos :x] 200
2.93969262078591
Efectivamente, existe una raíz de la ecuación en el intervalo (-200,200).
Podemos producir una gráfico de la función f utilizando los procedimientos de la biblioteca LogoFE.
borrapantalla
graflineas [] recorrido [[x] 0.01 * :x - cos :x] dominio [-200 200 100]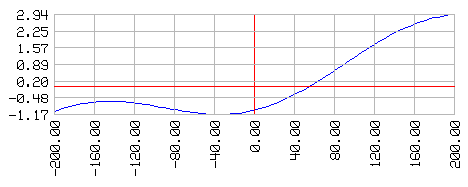
El método de bisección evalúa la función en el extremo izquierdo y derecho del intervalo. Luego calcula el valor intermedio entre los extremos y evalúa la función en este valor intermedio. Luego redefine el intervalo utilizando el valor intermedio, de tal manera que los valores de la función en los extremos del nuevo intervalo tengan diferente signo. El procedimiento imprime.linea nos muestra los resultados parciales:
para biseccion :f :iz :de
repite 10 [
haz "f_iz invoca :f :iz
haz "f_de invoca :f :de
haz "medio ( :iz + :de ) / 2
haz "f_medio invoca :f :medio
imprime.linea
si :f_medio * :f_iz < 0 [haz "de :medio]
si :f_medio * :f_de < 0 [haz "iz :medio]
]
fin
para imprime.linea
escribe `[( ,[formatonumero :iz 8 3] ,[formatonumero :de 8 3] )
f(iz): ,[formatonumero :f_iz 6 3]
f(de): ,[formatonumero :f_de 6 3]
medio: ,[formatonumero :medio 8 3]
f(medio): ,[formatonumero :f_medio 6 3]]
fin
Al ejecutar el procedimiento bisección en el intervalo (-200,200) obtenemos:
biseccion [[x] 0.01 * :x - cos :x] -200 200
( -200.000 200.000 ) f(iz): -1.060 f(de): 2.940 medio: 0.000 f(medio): -1.000
( 0.000 200.000 ) f(iz): -1.000 f(de): 2.940 medio: 100.000 f(medio): 1.174
( 0.000 100.000 ) f(iz): -1.000 f(de): 1.174 medio: 50.000 f(medio): -0.143
( 50.000 100.000 ) f(iz): -0.143 f(de): 1.174 medio: 75.000 f(medio): 0.491
( 50.000 75.000 ) f(iz): -0.143 f(de): 0.491 medio: 62.500 f(medio): 0.163
( 50.000 62.500 ) f(iz): -0.143 f(de): 0.163 medio: 56.250 f(medio): 0.007
( 50.000 56.250 ) f(iz): -0.143 f(de): 0.007 medio: 53.125 f(medio): -0.069
( 53.125 56.250 ) f(iz): -0.069 f(de): 0.007 medio: 54.688 f(medio): -0.031
( 54.688 56.250 ) f(iz): -0.031 f(de): 0.007 medio: 55.469 f(medio): -0.012
( 55.469 56.250 ) f(iz): -0.012 f(de): 0.007 medio: 55.859 f(medio): -0.003
Vemos cómo, inicialmente, el intervalo va de -200 a 200, posteriormente se reduce a la mitad: (0,200) y luego a la mitad (0,100). Así mismo, la función f va devolviendo valores cada vez más cercanos a cero para deferentes valores intermedios; inicialmente es -1.000 y luego de diez repeticiones es -0.003.
Al final de estas 10 repeticiones, el valor estimado para x es 55.859. Veamos cuán bien funciona x = 55.859 como raíz de la ecuación.
escribe cos 55.859
0.561231398520766
escribe 0.01 * 55.859
0.55859
cos(x) = 0.01 · x
0.56123 = 0.55859 (aproximadamente)
3. Adaptación Gráfica
Si dentro del procedimiento biseccion reemplazamos el comando imprime.linea por el comando dibuja.intervalo cuyo procedimiento está a continuación
para biseccion :f :iz :de
repite 10 [
haz "f_iz invoca :f :iz
haz "f_de invoca :f :de
haz "medio ( :iz + :de ) / 2
haz "f_medio invoca :f :medio
dibuja.intervalo
si :f_medio * :f_iz < 0 [haz "de :medio]
si :f_medio * :f_de < 0 [haz "iz :medio]
]
fin
para dibuja.intervalo
subelapiz ponx :iz
bajalapiz avanza 5 ponx :de retrocede 5 ponx :iz
subelapiz avanza 7
finobtenemos la representación gráfica de los sucesivos intervalos encontrados, al escribir lo siguiente en la línea de comandos de LogoFE:
borrapantalla
graflineas [] recorrido [[x] 0.01 * :x - cos :x] dominio [-200 200 100]
subelapiz pony 10 ponrumbo 0
biseccion [[x] 0.01 * :x - cos :x] -200 200
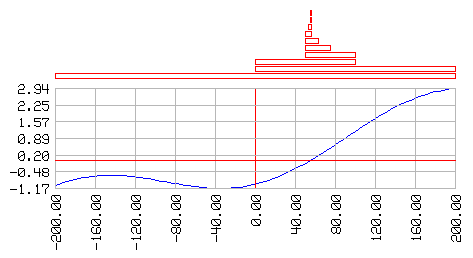
4. Mayor Precisión
Podemos mejorar la aproximación del valor de x modificando el procedimiento biseccion de tal manera que realize más repeticiones. Es más, podemos decirle que siga refinando la solución hasta que el intervalo sean tan estrecho como querramos:
para biseccion :f :iz :de
mientras [(abs :iz - :de) > 0.000000001] [
haz "f_iz invoca :f :iz
haz "f_de invoca :f :de
haz "medio ( :iz + :de ) / 2
haz "f_medio invoca :f :medio
si :f_medio * :f_iz < 0 [haz "de :medio]
si :f_medio * :f_de < 0 [haz "iz :medio]
]
devuelve :medio
fin
escribe biseccion [[x] 0.01 * :x - cos :x] -200 200
55.9670123468095
escribe cos 55.9670123468095
0.559670123476041
escribe 0.01 * 55.9670123468095
0.559670123468095
escribe formatonumero (0.559670123468095 - 0.559670123476041) 16 16
-0.0000000000079460
5. Aplicaciones
El procedimiento biseccion puede utilizarse para resolver muchos tipos de problemas. Por ejemplo, para resolver ecuaciones de una variable sin tener que despejar, para encontrar la raíz cuadrada de 2,
haz "x biseccion [[x] :x * :x - 2] 0 2
escribe :x
1.41421356145293
escribe :x * :x
1.99999999739737
para encontrar las raíces de un polinomio: f(x) = x5 + x4 - 3 x3 - 2
haz "f [[x] :x*:x*:x*:x*:x + :x*:x*:x*:x - 3*:x*:x*:x - 2]
borrapantalla
graflineas [] recorrido :f dominio [-2.5 2 100]
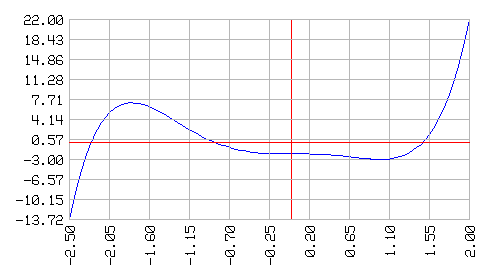
escribe biseccion :f -2.5 -2
-2.25364402215928
escribe biseccion :f -2 0
-0.862353793345392
escribe biseccion :f 0 2
1.46975488495082
escribe formatonumero (invoca :f -2.25364402215928) 10 10
0.0000000192
escribe formatonumero (invoca :f -0.862353793345392) 10 10
0.0000000049
escribe formatonumero (invoca :f 1.46975488495082) 10 10
0.0000000107
6. Licencia
Este es un documento libre.
Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.

