Curvas Fractales
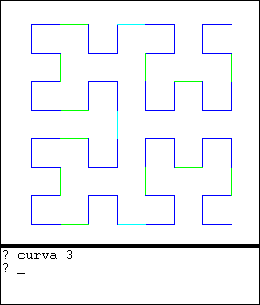
Las curvas fractales son dibujos que se definen repitiéndose a si mismos a diferentes niveles. Un ejemplo típico es la Curva de Hilbert. A continuación mostramos la construcción de una curva de Hilbert de orden 3 (o nivel 3) usando el lenguaje de programación Logo:
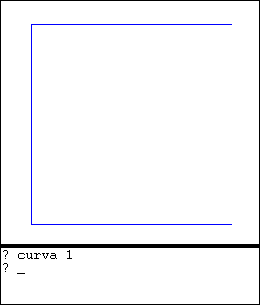
Estas curvas pueden ser dibujadas usando procedimiento recursivos, es decir procedimientos que se llaman a si mismos. La curva de Hilbert de orden 1 es la más sencilla y constituye el caso base. Podría definirse así:
para hilbert_1 | |
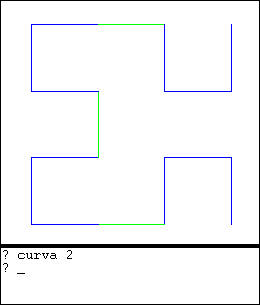
Usando la curva de orden 1 como base, podemos definir la curva de orden 2, así:
para hilbert_2 | |
Ya que ambos procedimientos tienen la misma estructura puede definirse un procedimiento general:
para hilbert :nivel :angulo
si :nivel < 1 [alto]
giraizquierda :angulo
hilbert :nivel - 1 (cambiasigno :angulo)
segmento
giraderecha :angulo
hilbert :nivel - 1 :angulo
segmento
hilbert :nivel - 1 :angulo
giraderecha :angulo
segmento
hilbert :nivel - 1 (cambiasigno :angulo)
giraizquierda :angulo
fin
para segmento
poncolorlapiz :nivel
avanza :tam
fin
Para centrar la curva fractal en la pantalla y para definir correctamente la longitud de cada segmento usamos el procedimiento curva:
para curva :nivel
haz "tam 200 / (-1 + potencia 2 :nivel)
borrapantalla
subelapiz ponpos [100 -70] bajalapiz
hilbert :nivel 90
fin
Los estructuras fractales en general tienen la propiedad de auto-similitud. Es decir que, si observamos una parte de la estructura como con un microscopio lo que observamos es similar, a lo que observamos a simple vista.
|
|
|
|
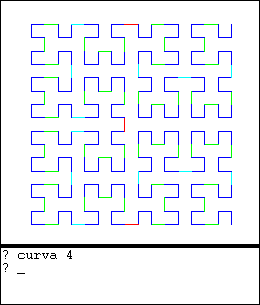
La curva fractal de Hilbert tiene la curiosa propiedad de que cuando el orden de la curva tiende al infinito, la curva tiende a cubrir el espacio. Es decir, el límite de esta curva unidimensional cubre un espacio bi-dimensional cuadrado.
|
|
1. Licencia
Este es un documento libre.
Autor: Daniel Ajoy
Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
2. Preguntas, Dudas, Comentarios, Peticiones
3. Enlaces
