Ejercicios de Matemáticas analizados con LogoFE

LogoFE es Logo Functional Extensions, una librería de procedimientos para ser usados con MSWLogo o con UCBLogo. El objetivo de LogoFE es proporcionar un gran "caja de herramientas" para la construcción de pequeños programas útiles o para explorar temáticas de Matemáticas, Física, Química, Estadística y otras materias de escuela, colegio y universidad.

Contenido

1. EJERCICIOS

La fuente de estos ejercicios es: Matemáticas Aplicadas a las Ciencias Sociales: Problemas Trimestre-1, Página-1.

1.1. Ejercicio 1

Compramos libros por valor de 6000 ptas.; si nos dieran tres libros más, me costarían 100 ptas. menos. ¿Cuántos libros he comprado?

Posible Solución

1. X * P = 6000
2. (X + 3) * (P - 100) = 6000

1. P = 6000 / X
2. (X + 3) * (P - 100) = 6000

1. P = 6000 / X
2. (X + 3) * (6000 / X - 100) = 6000

1. P = 6000 / X
2. (X + 3) * (6000 / X - 100) - 6000 = 0

Es probable que hayamos comprado más de un libro y quizá sean menos de 20.

Comprobemos:

Cada uno de los 12 libros nos costó 500 ptas. Si nos dieran 15 libros, y cada uno nos costó solamente 400 ptas, el costo total fue el mismo:

1.2. Ejercicio 2

Un país importa mensualmente 21000 vehículos de las marcas X, Y, Z, al precio de 1.2, 1.5 y 2 millones de pesetas, respectivamente. Si el total de la importación asciende a 32200 millones de ptas. y de la marca X se importa el 40% de la suma de las otras dos marcas, ¿cuántos vehículos de cada marca entran en el país?

Posible Solución

1. X + Y + Z = 21000
2. 1.2 X + 1.5 Y + 2 Z = 32200
3. X = 0.4 (Y + Z)

1. X + Y + Z = 21000
2. 1.2 X + 1.5 Y + 2 Z = 32200
3. X - 0.4 Y - 0.4 Z = 0

1. X = 6000
2. Y = 10000
3. Z = 5000

Comprobemos:

De las marcas Y e Z se importaron 15000 vehículos, el 40% de 15000 es 6000, que es la cantidad de vehículos importados de la marca X.

1.3. Ejercicio 3

Halla las edades de una persona, su padre y su abuelo, sabiendo que con su padre suma 55 años, con su abuelo 85, y que su padre y su abuelo suman 110 años.

Posible Solución

1. I + P = 55
2. I + A = 85
3. P + A = 110

1. 1 I + 1 P + 0 A = 55
2. 1 I + 0 P + 1 A = 85
3. 0 I + 1 P + 1 A = 110

1. I = 15
2. P = 40
3. A = 70

El Individuo tiene 15 años, el Padre tiene 40 y el Abuelo tiene 70 años.

1.4. Ejercicio 6

Resuelve las ecuaciones:

1. x³ + x = 0
2. x⁴ - x³ - 16x² - 20x = 0
3. x⁴ - 2x³ - 10x² + 4x + 16 = 0

Posible Solución

1. (x + 0) (x² + 1) = 0
2. (x + 2) (x + 2) (x - 5) = 0
3. (x + rc 2) + (x - rc 2) (x + 2) (x - 4) = 0

1. x = 0, x = -rc -1, x = rc -1
2. x = -2, x = -2, x = 5
3. x = -rc 2, x = rc 2, x = -2, x = 4

1.5. Ejercicio 7a

Resuelve el sistema:

1. x - y = 3
2. x² - xy = 15

Posible Solución

1. x = 3 + y
2. (3 + y)² - (3 + y) y - 15 = 0

Veamos más o menos por dónde se encuentran las raíces de la segunda ecuación:

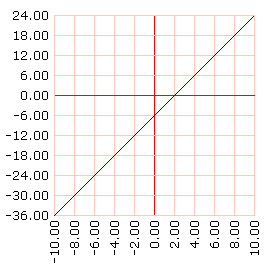
Parece ser una recta, y lo verificamos observando que el término elevado al cuadrado se anula en la expresión. Entonces la respuesta es:

Verificamos que:

1.6. Ejercicio 7b

Resuelve el sistema:

1. x² - xy = 8
2. y² - xy = -4

Posible Solución

Transformemos los ecuaciones para que puedan graficarse:

1. y = (x² - 8) / x
2. x = (y² + 4) / y

La primera ecuación puede graficarse como una función de x. Esta función tiene una asíntota en x = 0.

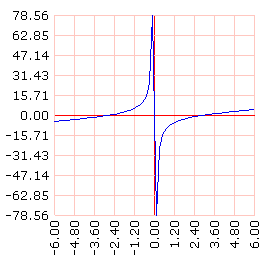
La segunda ecuación es una función de y. Esta función también tiene una asintota, en y = 0. Si consideramos el eje horizontal como el eje Y resulta:

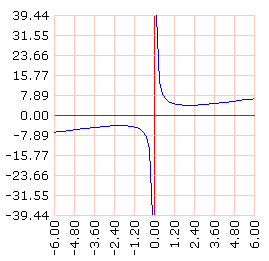
Pero para juntar ambas gráficas convendremos en que el eje horizontal sea el eje X y el vertical sea el eje Y. Por lo que la segunda ecuación se puede graficar así:

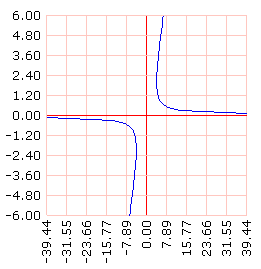
Al juntar ambas gráficas y definir adecuadamente el sector del plano cartesiano a mostrar, se puede apreciar las soluciones del sistemas de ecuaciones:

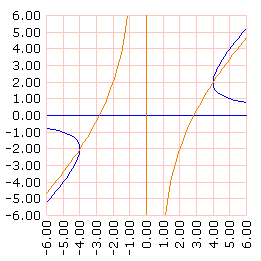
x = -4, y = -2

• x² - xy = 8 → (-4)² - (-4)(-2) = (-4)(-4) - (-4)(-2) = 16 - 8 = 8
• y² - xy = -4 → (-2)² - (-4)(-2) = (-2)(-2) - (-4)(-2) = 4 - 8 = -4

x = 4, y = 2

1. x² - xy = 8 → (4)² - (4)(2) = (4)(4) - (4)(2) = 16 - 8 = 8
2. y² - xy = -4 → (2)² - (4)(2) = (2)(2) - (4)(2) = 4 - 8 = -4

1.7. Ejercicio 14

Se sabe que el peso ideal correspondiente a las alturas de los hombres se rige por una función lineal. Sabemos que a una altura de 165 cm y a una de 170 cm, corresponden los pesos ideales de 68 kg y de 72 kg., respectivamente. Obtén por interpolación la función lineal correspondiente.

¿Cuál es el peso adecuado para un hombre que mide 172 cm? ¿Y cuál es la altura ideal de un hombre que tiene un peso de 70 kg?

Posible Solución

En un plano cartesiano de alturas versus pesos los puntos [165 68], [170 72] definen una recta (un polinomio de primer grado):

1. p = 0.8 a - 64
2. a = 1.25 p + 80

El peso adecuado para un hombre que mide 172 cm es 73.6 kg:

La altura ideal de un hombre que tiene un peso de 70 kg es 167.5 cm:

1.8. Ejercicio 21

El número de turistas que visitaron España en el periodo 1970 a 1985 siguió la siguiente tendencia: año 1970 - 24.1 millones de turistas, año 1975 - 30.1 millones de turistas, año 1980 - 38,1 millones de turistas, y 1985 - 43.1 millones de turistas. a) Halla la previsión para el año 1988 a partir de la función de interpolación lineal que obtienes a partir de los datos correspondientes a 1980 y 1985. b) Realiza la misma previsión utilizando el polinomio de interpolación de 2º grado (interpolación cuadrática) utilizando la información de los últimos tres años.

Posible Solución

Esta es la lista de datos que pueden ser representados como puntos en el plano cartesiano: [[1970 24.1] [1975 30.1] [1980 38.1] [1985 43.1]]

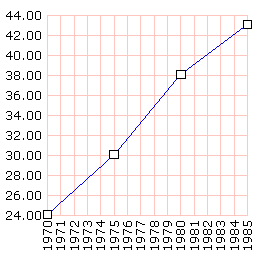
Utilizando los dos últimos puntos para definir una recta determinamos que la recta tendrá la siguiente ecuación.

f(x) = y = x - 1941.9

Y al evaluar la función para x = 1988, encontramos que el número de turistas proyectados para 1988 es 46.1 millones:

Utilizando los tres últimos años determinamos una parábola así:

f(x) = y = -0.0599992500093749 x² + 238.897030037125 x - 237756.959749253

Y al evaluar la función para x = 1988, encontramos que el número de turistas proyectados para 1988 es 44.7 millones:

Esto último podría graficarse así:

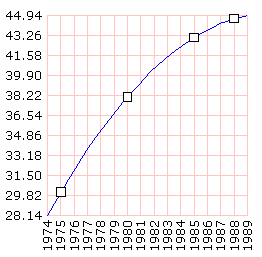
1.9. Ejercicio 25

Resuelve la siguiente ecuación:

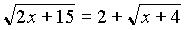
Posible Solución

Gráfiquemos ambos lados de la ecuación como si fuesen funciones. Pero primero averiguemos dónde se hacen cero las expresiones debajo de los radicales:

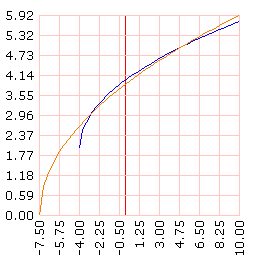
Una vez determinada la ubicación aproximada de las soluciones podemos hacer mejores aproximaciones:

1.10. Ejercicio 28

Resuelve la siguiente ecuación: 2x⁴ - 5x³ +5x - 2 = 0

Posible Solución

Así que todas son raíces reales: x = 0.5, x = 1, x = -1, x = 2

1.11. Ejercicio 29

Expresa el área de un triángulo rectángulo de perímetro 20 cm. en función de la longitud de la base. ¿Para qué longitud de la base el área será máxima?

Posible Solución

El perímetro de un triángulo rectángulo debe ser:

Si el perímetro del triángulo debe ser 20 cm. entonces si damos algún valor a un cateto (a la base) el otro cateto no podrá tener cualquier valor, sino que deberá tener un valor fijo.

El área de un triángulo es: base * altura / 2. Y en el caso de un triángulo rectángulo la base podría ser el un cateto y la altura el otro:

Finalmente grafiquemos el área del triángulo en función de la longitud de la base. Esta longitud no podrá ser menor a 0, ni tampoco mayor a 10 (porque en el caso extremo de que sea 10, la hipotenusa deberá ser igualmente 10 para que dicho "triángulo" tenga perímetro 20).

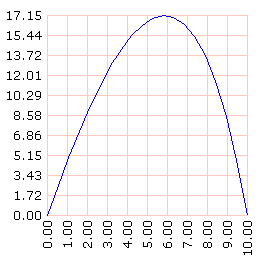
La longitud de la base para la que el área máxima del tríangulo parece estar cerca de 6. Pero en 6 el área ya se está reduciendo (ya que la taza de variación instantánea, la derivada, es negativa en 6).

Pero la solución está entre 5 y 7:

2. Licencia

Este es un documento libre.

Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.

3. Preguntas, Dudas, Comentarios, Peticiones

4. Enlaces

Ejercicios de Plano Cartesiano

---