Números Complejos, Aplicaciones
El dibujo de un automovil se puede representar como un conjunto de trazos. Al final de cada trazo es necesario levantar el lápiz. Cada trazo se puede representar por los puntos por donde pasa. Cada punto se puede representar como un número complejo. La siguiente es la presentación del dibujo de un auto. Cada línea de código siguiente representa un trazo:
haz "auto [
[[-16 -4] [-12 -4] [-8 0] [-8 4] [-12 8] [-16 8] [-20 4] [-20 0] [-16 -4]]
[[32 0] [32 12] [20 16] [16 24] [-20 24] [-28 12] [-28 0] [-20 0]]
[[8 0] [8 4] [12 8] [16 8] [20 4] [20 0] [16 -4] [12 -4] [8 0]]
[[0 12] [0 22] [14 22] [18 16] [18 12] [0 12]]
[[-22 12] [-4 12] [-4 22] [-18 22] [-22 12]]
[[32 10] [34 10] [34 6] [32 6]]
[[-8 0] [8 0]]
[[20 0] [32 0]]
]
El primer punto del primero trazo es -16-4i, que en LogoFE se representa simplemente como [-16 -4].
Usaremos el procedimiento dibujaTrazo para dibujarlos. Primero levantamos el lápiz y luego, vamos pasando por cada uno de los puntos del trazo ya con el lápiz abajo.
para dibujaTrazo :puntos
subelapiz
paracada :puntos [ponpos ? bajalapiz]
fin
Para dibujar el auto completo debemos dibujar varios trazos. Luego de dibujarlos ponemos la tortuga en el centro de la pantalla, para tener una referencia de la posición 0+0i:
borrapantalla
paracada :auto [dibujaTrazo ?]
subelapiz centro

Luce mejor si ocultamos la tortuga:
borrapantalla ocultatortuga
paracada :auto [dibujaTrazo ?]

Si a los puntos del auto, considerados como números complejos, les restamos 200 + 0i, logramos desplazar hacia la izquierda el auto 200 unidades.
muestra primero :auto
[[-16 -4] [-12 -4] [-8 0] [-8 4] [-12 8] [-16 8] [-20 4] [-20 0] [-16 -4]]
muestra primero primero :auto
[-16 -4]
muestra restacomp dista [200 0] primero primero :auto
[-216 -4]
muestra impon [restacomp dista [200 0]] primero :auto
[[-216 -4] [-212 -4] [-208 0] [-208 4] [-212 8] [-216 8] [-220 4] [-220 0] [-216 -4]]
muestra impon [impon [restacomp dista [200 0]]] :auto
[[[-216 -4] [-212 -4] [-208 0] [-208 4] [-212 8] [-216 8] [-220 4] [-220 0] [-216 -4]]
[[-168 0] [-168 12] [-180 16] [-184 24] [-220 24] [-228 12] [-228 0] [-220 0]]
[[-192 0] [-192 4] [-188 8] [-184 8] [-180 4] [-180 0] [-184 -4] [-188 -4] [-192 0]]
[[-200 12] [-200 22] [-186 22] [-182 16] [-182 12] [-200 12]]
[[-222 12] [-204 12] [-204 22] [-218 22] [-222 12]]
[[-168 10] [-166 10] [-166 6] [-168 6]]
[[-208 0] [-192 0]]
[[-180 0] [-168 0]]
]
borrapantalla muestratortuga
paracada impon [impon [restacomp dista [200 0]]] :auto [dibujaTrazo ?]
subelapiz centro

Podemos mover el auto horizontalmente si a cada número complejo le sumamos un número complejo de la forma x + 0i, de tal manera que x vaya desde -200 hasta 200 en pasos de 10 en 10:
desde [x -200 200 10] [
borrapantalla
paracada impon [impon [sumacomp lista (lista :x 0)]] :auto [dibujaTrazo ?]
subelapiz centro
]

Y si con sumas y restas de números complejos podemos mover objetos en el plano cartesiano. Con multiplicaciones podemos agrandar o empequeñecer objetos. Por ejemplo, si a los números que representan un objeto les multiplicamos por un número de la forma x + 0i, de tal manera que x vaya desde 0.1 hasta 2.0 en pasos de 0.1 en 0.1, podemos hacer un efecto de magnificación:
haz "hormiga [
[[4 36] [12 28] [28 24] [44 24] [56 36] [56 44] [44 56] [28 56] [12 52] [4 44]]
[[-20 32] [0 32] [4 36] [4 44] [0 48] [-20 48] [-28 44] [-28 36] [-20 32]]
[[-28 36] [-36 28] [-44 28] [-48 32] [-52 48] [-44 56] [-32 52] [-28 44]]
[[-40 36] [-40 44] [-44 44] [-44 40] [-40 36]]
[[-40 0] [-32 8] [-32 20] [-20 32]]
[[-16 32] [-8 20] [-8 8] [0 0]]
[[-4 32] [0 24] [16 8] [20 0]]
[[-48 48] [-68 56] [-72 28]]
[[-44 56] [-52 64] [-60 36]]
[[36 28] [32 40] [36 52]]
[[48 28] [44 36] [48 48]]
[[28 56] [20 40] [24 28]]
]
desde [x 0.1 2.0 0.1] [
borrapantalla
paracada impon [impon [multicomp lista (lista :x 0)]] :hormiga [dibujaTrazo ?]
subelapiz centro
]

A continuación mostramos los números complejos que usamos en este efecto de magnificación y sus respectivas magnitudes y ángulos:
; [Real Imaginario] --> [Magnitud Angulo]
desde [x 0.1 2 0.1] [(escribe lista :x 0 "--> recpol lista :x 0)]
[0.1 0] --> [0.1 0]
[0.2 0] --> [0.2 0]
[0.3 0] --> [0.3 0]
[0.4 0] --> [0.4 0]
[0.5 0] --> [0.5 0]
[0.6 0] --> [0.6 0]
[0.7 0] --> [0.7 0]
[0.8 0] --> [0.8 0]
[0.9 0] --> [0.9 0]
[1 0] --> [1 0]
[1.1 0] --> [1.1 0]
[1.2 0] --> [1.2 0]
[1.3 0] --> [1.3 0]
[1.4 0] --> [1.4 0]
[1.5 0] --> [1.5 0]
[1.6 0] --> [1.6 0]
[1.7 0] --> [1.7 0]
[1.8 0] --> [1.8 0]
[1.9 0] --> [1.9 0]
Vemos que la magnitud es idéntica a la parte real de cada complejo. Esto no debería sorprendernos, ya que la parte imaginaria es nula en cada número. También vemos el ángulo siempre es 0. La magnitud varía y el ángulo es constante.
Podemos hacer lo contrario, es decir, variar el ángulo de los números pero mantener constante la magnitud:
; [Magnitud Angulo] <-- [Real Imaginario]
desde [ang 0 -90 -10] [(escribe lista 1 :ang "<-- polrec lista 1 :ang)]
[1 0] <-- [1 0]
[1 -10] <-- [0.984807753012208 -0.17364817766693]
[1 -20] <-- [0.939692620785908 -0.342020143325669]
[1 -30] <-- [0.866025403784439 -0.5]
[1 -40] <-- [0.766044443118978 -0.642787609686539]
[1 -50] <-- [0.642787609686539 -0.766044443118978]
[1 -60] <-- [0.5 -0.866025403784439]
[1 -70] <-- [0.342020143325669 -0.939692620785908]
[1 -80] <-- [0.17364817766693 -0.984807753012208]
[1 -90] <-- [6.1257422745431e-17 -1]
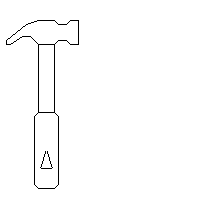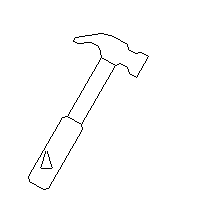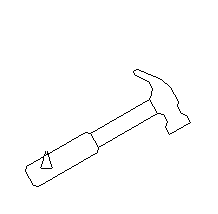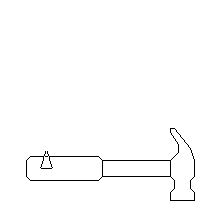
Al utilizar estos números complejos para multiplicarlos por los números complejos que representan un martillo obtenemos un efecto de rotación:
haz "martillo [
[[-12 -16] [-8 -20] [8 -20] [12 -16] [12 52] [8 56] [-8 56] [-12 52]
[-12 -16]] [[-8 56] [-8 124]] [[8 124] [8 56]] [[-40 128] [-40 124]
[-36 124] [-24 132] [-16 132] [-12 128] [-8 124] [8 124] [12 128] [20 128]
[24 124] [32 124] [32 148] [24 148] [20 144] [12 144] [8 148] [-8 148]
[-20 144] [-40 128]]
]
desde [ang 0 -90 -10] [
borrapantalla
paracada impon [impon [multicomp lista polrec lista 1 :ang]] :martillo [dibujaTrazo ?]
subelapiz centro
]
1. Licencia
Este es un documento libre.
Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
2. Preguntas, Dudas, Comentarios, Peticiones
3. Enlaces
Proyectos de Matemáticas de Planos Cartesianos

