Torneo de Computación y Matemática - Nivel 2

8mo Torneo de Computación y Matemática
Nivel 2 (9no y 10mo año de escolaridad)
Ronda Final

Contenido

1. Pregunta 1

Encontrar todas las soluciones enteras positivas de

x² + y³ + z⁴ = 20052005

1.1. Posible Solución

x = RaízCuadrada(20052005 - y³ - z⁴)

La siguiente función devuelve un valor de x con el cual se cumple la ecuación planteada (aunque este valor puede ser no entero), o en caso de que se pretenda sacar la raíz cuadrada de un número negativo, la función devuelve un valor fraccionario, ya que pensamos descartar todos los valores fraccionarios devueltos por esta función:

Encontramos valores máximos de y y z, y los usamos para encontrar las soluciones:

Los anteriores son los valores de y y z que producen valores de x enteros. Los siguientes son los correspondientes valores de x:

Comprobación:

2. Pregunta 2

Algunos números enteros positivos no se pueden escribir como suma de dos cuadrados perfectos (1, 4, 9, 16, 25, 36, etc.). Otros sí. Algunos se pueden escribir de varias formas distintas. Por ejemplo 50 = 1+49 = 25+25 se puede escribir de dos formas distintas. 1+49 es la misma forma que 49+1. Notar que 50 es múltiplo de 5.

1. ¿Cuántos enteros de 1 a 1000 se pueden escribir de 2 (dos) o más formas distintas como suma de dos cuadrados, pero no son múltiplos de 5?
2. ¿Cuántos enteros de 1 a 10000 se pueden escribir de 3 (tres) o más formas distintas como suma de dos cuadrados, pero no son múltiplos de 5?
3. ¿Cuántos enteros de 1 a 100000 se pueden escribir de 4 (cuatro) o más formas distintas como suma de dos cuadrados, pero no son múltiplos de 5?

2.1. Posible Solución

Vemos que sólo debemos tratar con los números hasta n = RaizCuadrada N / 2

Esta es la tabla completa, pero ya que "1+49 es la misma forma que 49+1" entonces debemos tener en cuenta eso y nos interesarán, para la pregunta a, los que tengan 3 repeticiones o más, o lo que es lo mismo, más de 2 repeticiones. Ordenamos los números y los agregamos:

Los contamos y fitramos los que tienen 3 o más repeticiones:

Luego sólo nos interesan los que no son múltiplos de 5:

Definimos una función que nos conteste las preguntas:

La respuesta de b:

La respuesta de c:

3. Pregunta 3

Dados los enteros no negativos A, B y M, a partir de un término inicial x0 se construye la sucesión

x_i+1 = (A · x_i + B) mod M

donde mod es el resto de la división entera (16 mod 3 = 1, 6 mod 2 = 0, etc.)

Se buscan valores de M tales que

• los números x₀, x₁, x₂, ..., x_M-1 son todos distintos,
• x_M = x₀ , y además
• 4 · (x₀ · x₁ + x₁ · x₂ + x₂ · x₃ + ... + x_M-1 · x_M) = M · (M-1)²

1. Encontrar dos valores de M que estén entre 10 y 100
2. Encontrar dos valores de M que estén entre 100 y 1000

Para cada uno de los cuatro valores de M encontrados, dar también un valor de A y B tales que se cumpla lo pedido.

Ejemplo 1: si A = 9, B = 2, y M = 12, una sucesión posible es x₀ = 3, x₁ = 5, x₂ = 11, x₃ = 5, ... En este caso no son todos distintos.

Ejemplo 2: si A = 1, B = 1, y M = 4, una sucesión posible es x₀ = 0, x₁ = 1, x₂ = 2, x₃ = 3, (x₄ = 0) En este caso 4 · ( x₀ · x₁ + x₁ · x₂ + x₂ · x₃ + x₃ · x₄) = 4(0 + 2 + 6 + 0) = 32, mientras que M · (M-1)² = 36, así que no se cumple la tercera condición.

3.1. Posible Solución

Primero creamos una función que devuelva la sucesión dados un x₀, a, b y m. Los xs hay que leerlos de derecha a izquierda.

Para tener una idea del problema también programamos este procedimiento, que nos muestra qué tan bien cumple la sucesión generada con respecto a las restricciones. La primera línea es la sucesión, la segunda son los elementos diferentes de la sucesión, la tercera son los valores de la tercera condición (deberían ser iguales):

En lo anterior, vemos que a no influye en el número de elementos diferentes de una sucesión.

En lo anterior, vemos que b puede variar los valores de la tercer condición, pero que al hacerlo puede afectar la primera condición.

En lo anterior, vemos que, para m=7, b puede variar los valores de la tercer condición, pero esto no altera el cumplimiento de la primera y segunda condiciones. b debe ser menor que m. Nos percatamos que 7 es primo.

Definimos una función que nos diga si se cumple la tercera condición para una pareja de valores [b m]

f3 nos devuelve 0 si para una pareja de valores [b m], la tercera condición no se cumple, caso contrario 1.

Ningún, valor de b fuciona para m=7:

Definimos una función f3bs que nos diga para cuántos valores de b la tercera condición se cumple para una valor de m dado:

Buscamos entre los primos entre 10 y 100:

Bingo! Ahora a encontrar los bs.

Es decir, para la pregunta a, hay las siguientes soluciones:

• a=1, b=4, m=19
• a=1, b=15, m=19
• a=1, b=15, m=71
• a=1, b=56, m=71

Pero luego cuando intentamos hacer los mismo para el rango de la pregunta b no obtenemos ninguna respuesta:

Al ver las respuestas de la pregunta a notamos un patrón, por el cual la siguiente b podría ser 56. Buscamos todos los ms entre 100 y 1000 que pudieran cumplir con la tercera condición, dado un b=56:

• a=1, b=56, m=265
• a=1, b=209, m=265

Luego debería existir un número m para un b=209:

• a=1, b=209, m=989
• a=1, b=780, m=989

4. Pregunta 4

Una calculadora muestra cada número utilizando 7 segmentos, como se muestra en la figura:

4.1. Posible Solución

Definimos un diccionario, que asocie cada dígito con su respectivo número de segmentos. Si buscamos en el diccionario el dígito 1 vemos que la cantidad de segmentos que tiene es 2. Si buscamos en el diccionario el dígito 7 vemos que la cantidad de segmentos que tiene es 4:

Dado un número de varios dígitos, buscamos el número de segmentos de cada uno. Por ejemplo, con 107:

Sumamos dichas cifras. A toda esta funciona la llamamos total

Vemos que total funciona para el número 107 y nos indica que para mostrarse necesita 12 segmentos:

Cuáles son algunos múltiplos de 107:

Intentamos varios de ellos hasta encontrar uno que tenga 16 segmentos:

5. Pregunta 5

Agustín quiere llenar el siguiente tablero de 4x4 con números enteros distintos de manera que el número que está en cada casilla sea un múltiplo del número que está en la casilla que está a su izquierda y de la casilla que está abajo. Y además se quiere que en la esquina inferior izquierda esté el número 1, en la esquina superior derecha este el número 192433829.

5.1. Posible Solución

Ya que el número de la esquina superior derecha debe ser el múltiplo de varios otros vemamos cuáles son los factores primos que lo componen:

El trabajo de exploración se haría más facilmente usando una hoja electrónica. A falta de ella simularemos su funcionamiento para una matriz a de dimensión 5x5. Donde están los ceros calcularemos el mínimo común multiplo de la casilla que está a la izquierda y de la casilla que está abajo. De esta forma, las casillas que tienen ceros luego cumplirán un requisito de Agustín.

Usaremos otra matriz b que tenga factores adicionales que ubicaremos estratégicamente para hacer que las casillas de a sean diferentes de 1

6. Pregunta 6

Se tienen tiras de caritas en fila. Algunas están bien y otras están al revés. Una carita del medio es feliz si alguna de sus dos vecinas mira para el mismo lado. Una carita de la punta es feliz si su única vecina mira para el mismo lado.

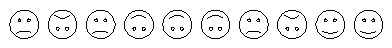
En el ejemplo de la figura hay 5 caritas felices: 2 bien y 3 al revés.

a) Consideramos todas las posibles filas que tienen 5 caritas para arriba y 5 para abajo. ¿Cuál es el promedio de caritas felices?

b) ¿Y si consideramos las filas con 10 y 10 caritas?

6.1. Posible Solución

Trataremos de definir una función que nos diga cuantas caras son felices dada una fila. Primero parcharemos los extremos de la fila con cruces:

Ahora hacemos grupos de 3, de la cara y las vecinas:

Trabajemos con un grupo. Comparamos la cara con las vecinas. Si son iguales la comparación devolverá 1. Combinamos las dos comparaciones sumándolas:

De esta manera definimos la función alegre?

Vemos que sería mejor modificar la función alegre? para que nos devuelva sólo 0 si la cara no está alegre o 1 si sí lo está:

De esta menara podremos sumar las caras alegres así:

En un principio teníamos la idea de encontrar todas las permutaciones de 10 elementos de esta secuencia [r r r r r b b b b b]. Pero vemos que sería muchas, y se repetirían:

Por ejemplo:

[r1 r2 r3 r4 r5 b1 b2 b3 b4 b5]

[r2 r1 r3 r4 r5 b1 b2 b3 b4 b5]

Serían dos permutaciones distintas pero para nuestros propósitos serían iguales. Buscamos otro método. Vemos que las posibles combinaciones de 5 elementos a partir de 10 elementos son muchas menos. Las calculamos:

Vemos que, si consideramos a estos números como índices que nos dicen la posición de las caras hacia arriba, podemos crear filas similares a las que teníamos antes. Y vemos que cuentafelices también nos sirve para contar este tipo de filas:

Es decir, 20/3.

Es decir, 130/19.

7. Preguntas, Dudas, Comentarios, Peticiones

8. Enlaces

Soluciones de Problemas de otros niveles

---