El problema de la oveja tragona
1. El problema
Supongamos que tenemos un campo circular y en uno de los postes de su perímetro se encuentra atada una oveja, tal vez era de esas que comen mucho pasto. Se desea conocer la longitud que tiene que tener la soga que ata a la oveja para solo pueda deglutir la mitad del área del campo. Obtenido de "La oveja voraz y el campo circular".
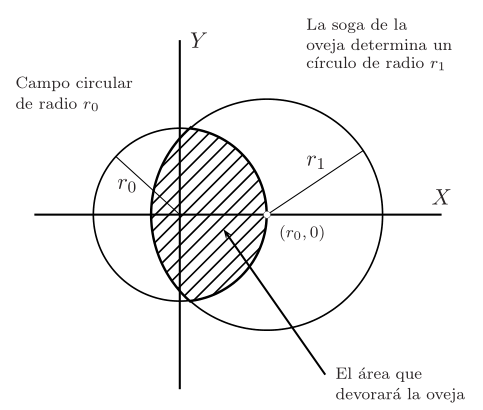
2. Otra Solución
Aquí, estoy graficando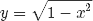 
. Eso sería la mitad del círculo de arriba.
bp graflineas [] recorrido [rc 1 - ? * ?] dominio [-1 1 100]
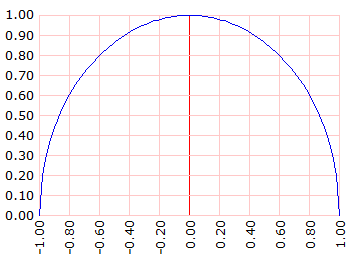
Lo mismo pero extendiendo la gráfica hasta 3 y haciendo que la raíz cuadrada no se queje.
bp graflineas [] recorrido [rc max lista 0 1 - ? * ?] dominio [-1 3 100]
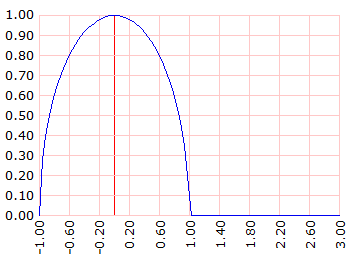
Ahora también graficamos la mitad del otro círculo, para el ejemplo digamos que el largo de la soga es 1.5.
bp graflineas [] tabula [
? [rc max lista 0 1 - ? * ?]
? [rc max lista 0 1.5 * 1.5 - (? - 1) * (? - 1)]
] dominio [-1 3 100]
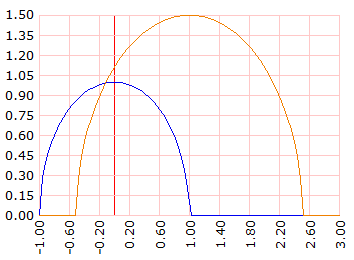
Esto es el mínimo de ambas curvas. El área bajo la curva será la mitad de lo que se traga la oveja.
bp graflineas [] tabula [? [min lista
(rc max lista 0 1 - ? * ?)
(rc max lista 0 1.5 * 1.5 - (? - 1) * (? - 1))
]] dominio [-1 1 100]
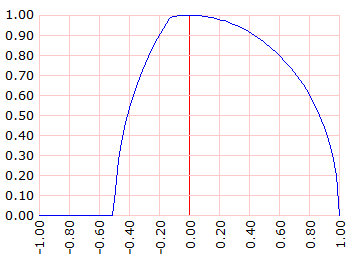
Esto sería lo que la oveja se come si la longitud de la soga fuese 1.
bp graflineas [[Ymax: 1]] tabula [? [min lista
(rc max lista 0 1 - ? * ?)
(rc max lista 0 1 * 1 - (? - 1) * (? - 1))
]] dominio [-1 1 100]
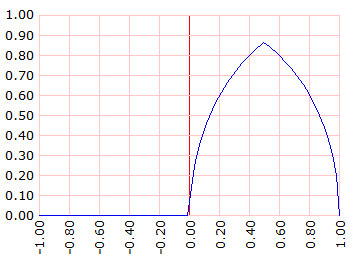
Aquí definimos una función f en la que volvemos variable el largo de la soga (variable m). Además, que devuelva el área que la oveja se come (el doble del área de los gráficos anteriores) dividido para el área del campo circular de pasto (π x r02 = π x 1 = π).
Así, la función f nos dice qué fracción del área del campo circular de pasto se come la oveja dependiendo del largo de la soga.
funciona "f [invoca [[m] 2 / pi * integra [invoca [min lista
(rc max lista 0 1 - ? * ?)
(rc max lista 0 :m * :m - (? - 1) * (? - 1))
]] [-1 1]]]
Si el largo de la soga es 0, la oveja no puede comer nada. Además queda ahorcada.
muestra f 0
0
Si el largo de la soga es 2, la oveja se como todo.
muestra f 2
0.999999999820495
Si el largo de la soga es 1, la oveja se come menos de la mitad.
muestra f 1
0.391002218857384
Buscamos cuánto debe ser el largo de la soga para que la oveja se coma la mitad del campo. El número que buscamos definitivamente debe estar entre 0 y 2.
muestra resuelve [0.5 - f] [0 2]
1.15872847320392
muestra f 1.15872847320392
0.500000000000003
Esta función f es la mismísima función Ω del árticulo del que sacamos el problema, pero sin necesidad de resolver integrales, buscar límites de integración, ni nada de esa cosa fea. Igual, a la final, Sebastián también usó métodos numéricos para encontrar este resultado.
3. Licencia
Este es un documento libre.
Autor: Daniel Ajoy
Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
4. Preguntas, Dudas, Comentarios, Peticiones
5. Enlaces
