Resolviendo un problema de maximización usando Logo
Contenido
1. Parte 1
From: Daniel Ajoy, dajoy at openworldlearning.org
Date: Thu, 16 Dec 1999 15:31:41 -0500
Waldo, wdiaz at iie.ufro.cl escribió:
En ese periodo colaboré con un profesor español que me facilitó por algunos dias, libros sobre uso de Logo en niveles terciarios, es decir universidad, me resulto fascinante esa lectura, debido a la utilidad que presta este programa para el trabajo de cálculo, es decir, derivadas e integrales
Hace algun tiempo apareció en la lista Logo-L un mensaje con este encabezado.
Para los interesados en el original pueden buscarlo en el "archive" de ellos.
From: Yehuda
Date: Tue, 06 Oct 1998 15:01:59 +0200
Subject: LOGO-L> Solving a Max Problem Using Logo
Dice resumida y traducidamente:
Para resolver un problema de maximización o minimización generalmente necesitamos cálculo. Pero si tenemos Logo podemos resolver este tipo de problemas con estudiantes mucho más jóvenes.
Aquí está un problema de ejemplo:
Creamos una caja abierta de un cartón cuadrado. Que mide de lado 30 unidades. Para hacer esto, cortamos de cada esquina un cuadrado de logitud x unidades - todos los cuadrados son iguales - y luego doblamos el cartón por las lineas de corte. Luego de los dobleces tenemos una caja sin tapa de base cuadrada:
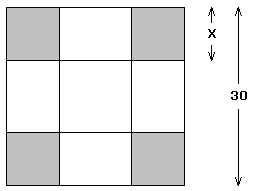
El problema es:
Cuál debe ser el valor de X de tal forma que el volumen de la caja sea el mayor posible.
Antes de seguir, conviene preguntarnos: Existe alguna solución? Existen muchas soluciones? Existe una única solución?
...
Todo lo que debemos hacer ahora es escribir un programa en Logo que calcule un valor numérico para x, que nos ayude a solucionar el problema.
El autor del mensaje luego de algunos días propone una alternativa realmente muy razonable. Creo yo que así lo resolvería una persona que no ha tenido contacto con el cálculo.
Mientras tanto quisiera saber qué opinan del problema? Qué tan complicado lo ven las personas que no han recibido mucho (o nada) de cálculo? Qué tan complicado le ven al problema los profesores para sus alumnos de 13-18 años? Cómo creen que se podría resolverse? Con Logo?
Daniel
2. Parte 2
From: Daniel Ajoy, dajoy at openworldlearning.org
Date: Tue, 21 Dec 1999 14:55:23 -0500
Hablemos con números, digamos que los cuadrados que quitamos eran de lado igual a 3. A continuación se muestra cómo se vería la caja cortada, la vista superior y la vista de lado.
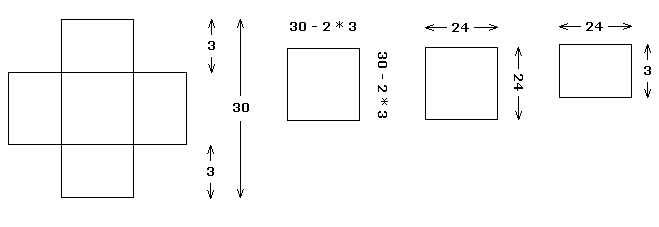
La superficie del cuadrado de la base es LADO x LADO:
haz "ladoCarton 30
haz "ladoCuadrados 3
haz "ladoBaseCaja :ladoCarton - 2 * :ladoCuadrados
escribe :ladoBaseCaja
24
haz "superficieBase :ladoBaseCaja * :ladoBaseCaja
escribe :superficieBase
576
El volumen de la caja es SUPERFICIE x ALTURA
haz "alturaCaja :ladoCuadrados
escribe :alturaCaja
3
haz "volumenCaja :alturaCaja * :superficieBase
escribe :volumenCaja
1728
Pongamos esto dentro de un procedimiento:
para volumen :ladoCarton :ladoCuadrados
haz "ladoBaseCaja :ladoCarton - 2 * :ladoCuadrados
haz "superficieBase :ladoBaseCaja * :ladoBaseCaja
haz "alturaCaja :ladoCuadrados
haz "volumenCaja :alturaCaja * :superficieBase
devuelve :volumenCaja
fin
Probemos nuestro procedimiento
escribe volumen 30 3
1728
Ese es el volumen de una caja de cartón cuadrada de lado 30 al que se le han quitado cuatro cuadrados de lado 3.
escribe volumen 30 7
1792
Ese es el volumen de una caja de cartón cuadrada de lado 30 al que se le han quitado cuatro cuadrados de lado 7.
Repasemos "cuentarepite" que guarda la cuenta de cada repetición:
repite 5 [escribe 2]
2
2
2
2
2
repite 5 [escribe cuentarepite]
1
2
3
4
5
repite 3 [escribe cuentarepite]
1
2
3
repite 3 [escribe 2 * cuentarepite]
2
4
6
Repasemos listas:
escribe lista 3 volumen 30 3
3 1728
Es la lista formada por el número 3 y el resultado del procedimiento volumen con datos 30 y 3.
Ahora sí, agárrese quien pueda :)
repite 16 [escribe lista cuentarepite volumen 30 cuentarepite]
Eso se traduce en:
escribe lista 1 volumen 30 1
escribe lista 2 volumen 30 2
escribe lista 3 volumen 30 3
...
escribe lista 16 volumen 30 16
Que tiene por resultado:
1 784
2 1352
3 1728
4 1936
5 2000
6 1944
7 1792
8 1568
9 1296
10 1000
11 704
12 432
13 208
14 56
15 0
16 64
De los resultados de los 16 experimentos se ve que cuando el lado de los cuadrados que se extraen es de 5, el volumen de la caja es el máximo: 2000.
[15 0] Es una caja sin base porque al cartón de 30 unidades de lado se le quita cuatro cuadrados de 15 unidades. No queda nada con qué hacer la caja.
También, un caso que no aparece es:
escribe lista 0 volumen 30 0
0 0
que es el cartón sin ningún corte. Si no hay cortes no pueden levantarse los lados. La caja no tiene lados, no tiene altura, por lo tanto no tiene volumen.
Daniel

