Superficie de Segmento Circular

LogoFE es Logo Functional Extensions, una librería de procedimientos para ser usados con MSWLogo o con UCBLogo. El objetivo de LogoFE es proporcionar un gran "caja de herramientas" para la construcción de pequeños programas útiles o para explorar temáticas de Matemáticas, Física, Química, Estadística y otras materias de escuela, colegio y universidad.

Contenido

El medidor de combustible de un camión de 18 ruedas no funciona, así que su conductor usa una varilla para medir el diesel en su tanque que tiene la forma de un cilindro acostado de 20 pulgadas de diámetro. Con esto el conductor puede fácilmente determinar que el tanque está medio lleno cuando la varilla se moja 10 pulgadas, pero ¿cuántas pulgadas debe mojarse la varilla si el tanque está 1/4 lleno?

1. Posible Solución

El problema es equivalente a calcular la superficie de un segmento circular ya que cuando varía el volumen del diesel en el tanque varía únicamente la superficie del segmento circular mojada por el diesel. La longitud del tanque se mantiene constante.

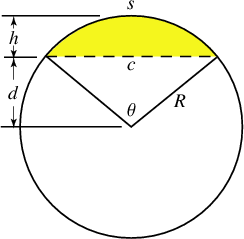
La determinación de la fórmula para tal superficie en función del radio R del círculo y de h está detallada en la siguiente referencia:

y es:

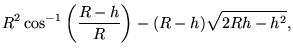
Calculemos cuánto sería ¼ de la superficie de un círculo de 20 pulgadas de diámetro D, conociendo que:

1. R = D / 2
2. S = ¼ · pi · R · R

Algo más de 78 pulgadas cuadradas. Utilizando la fórmula dada podemos intentar diferentes valores para h. Pero para esto debemos asegurarnos que contamos con la función arcocoseno en radianes. Si no contamos con ella, podemos definirla así:

A continuación calculamos las superficies del segmento circular para varios valores de h (la longitud mojada de la varilla).

Vemos que la respuesta a nuestro problema se halla entre 5 y 6. Esto lo podemos graficar así:

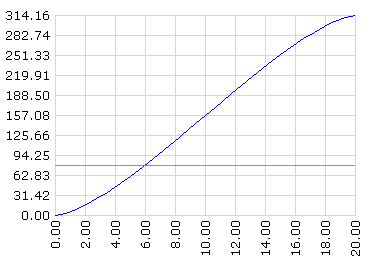
Una mejor aproximación podría calcularse así:

Para llegar a este resultado el Algebra resulta inútil ya que no es posible despejar el valor de h en la fórmula dada anteriormente. Es más, tampoco es necesario hacer todo aquel desarrollo para determinar la fórmula de la superficie del segmento circular en función de R y h. Unicamente es necesario saber: que integrar es equivalente a calcular el área bajo un curva, con qué función se puede graficar medio círculo, cómo hundir esta función un poco y cómo parcharla otro poco.

Aquí está la fórmula de la función de medio círculo:

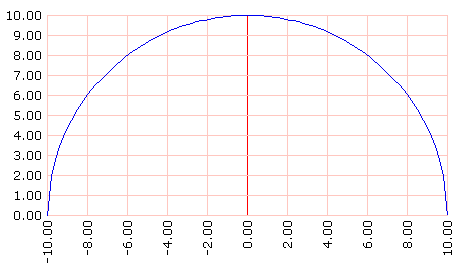
Esta es la manera de hundirla:

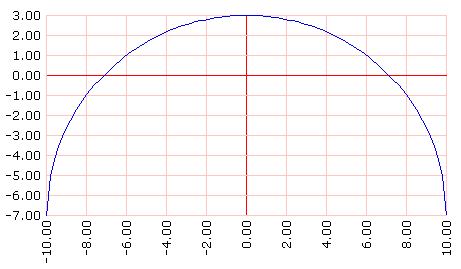
Esta es la forma de parcharla:

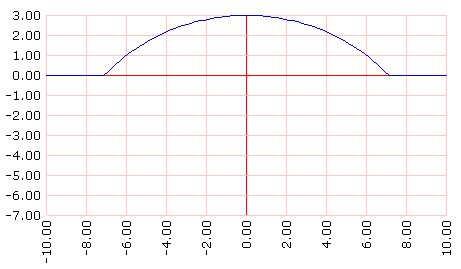
Entonces la superficie del segmento circular en función de h será:

Y el valor de h tal que la superficie sea S14 será:

2. Tabla para Calcular el Volumen de un Tanque Elíptico

3. Comentario 1

Hola Daniel,

No he podido dejar de sonreir al leer tu mensaje.

Me explico. Antes de estudiar matemáticas y dedicarme a la enseñanza, realicé estudios de náutica y durante varios años trabajé de mecánico en buques mercantes. En cierta ocasión la naviera compró en Holanda un barco de segunda mano y no había planos de sus tanques de combustible. Los dos que tenía, uno a cada banda, eran precisamente cilíndricos y estaban recostados, como los de tu camión, de forma que la sonda aparecía mojada de gas-oil, pero nadie era capaz de hacerse una idea de cuánto combustible había en los tanques. El jefe de máquinas, el capitán y el primer oficial se devanaban los sesos con los dichosos depósitos. Cuando me enteré de sus cuitas, puse manos a la obra y les hice una tabla: tantos cms., tantos litros.

...Ya han pasado unos años; si el cascarón aquel no se fue a pique o se lo llevaron al desguace, aun estarán con la tablita.

Realmente esto prueba que el problema es muy, pero que muy de la vida real.

Para deducir la fórmula:

Si r era el radio del depósito en cm, (x-r)² + y² = r²

era la circunferencia de la base centrada sobre el punto (r, 0).

Si la varilla estaba mojada x cm, la superficie mojada de la base venía dada por dos veces la integral de la función

y = (2 r t - t²)^½

en el intervalo (0, x)

A partir de aquí hice trampa. Tenía acceso a un ordenador (¡¡de 30 megas de disco duro!!) y a un programa de cálculo numérico que se llamaba Eureka; él fue quien me hizo la tabla integrando numéricamente, creo que por el método de Simpson, para diferentes valores de x.

Te diré que el conocido método de cuadratura de Simpson se expone en casi todos los manuales de la asignatura de "Construcción Naval y Teoría del Buque" que se imparte en las escuelas de náutica. Es práctica relativamente común en los barcos tener que calcular superficies o cubicar espacios de contornos más o menos irregulares, debido a la forma hidrodinámica del casco, y para las que no existen, o no se tienen a mano, expresiones analíticas de las curvas a integrar.

Acabo de poner al Mathematica a calcular la integral simbólicamente y sale una expresión más bien poco simpática. Lástima no disponer de esta herramienta en aquellos tiempos, ... igual si la enseñaba me aumentaban el sueldo.

4. Comentario 2

Señores

Buscando en la RED cosas interesantes de las matematicas, encontré esta pagina.- y al ver los comentarios de ustedes, no pude evitar agregar también mi comentario al respecto.

Como tecnico en mantenimiento de maquinas de emergencia, es mi responsabilidad recibir el surtido de diesel, corroborando que lo agregado al tanque, sea lo mismo que dice la hoja de pedido.

Igualmente que sus ejemplos.- Los tanques que tiene la empresa están en posicion horizontal.

Hace alrededor de 6 ó 7 años tuve que resolver este problema.

Para esta fecha, tal vez ya han encontrado una solución mejor.- Aún así, agregaré la mia.

Para calcular el volumen de diesel en cualquier punto de nivel del tanque, necesitamos partir de la sig formula.

V = A·L

El area del segmento circular puede calcularse con la sig formula:

A = ( π · r² · N/360 ) - ( c·(r-h)/2 )

Donde:

Como no podemos estar midiendo el angulo para cada nivel calculado, lo reemplazaremos con la siguiente formula:

N = 2 · ArcCos( r-h/r )

Tampoco necesitamos estar midiendo la cuerda si utilizamos la siguiente formula:

c = 2 · ( r² - (r-h)² )^½

Ahora... volvemos a la formula para calcular el area del segmento circular y reemplazamos "N" y "c" con sus respectivas formulas

Luego... vamos a la formula para calcular el volumen y reemplazamos "A" con lo obtenido anteriormente.

Por ultimo, como podran ver, obtuvimos una formula para calcular el volumen, de un tamaño que asusta.

Pero tiene la siguiente Ventaja:

Sólo tiene las incognitas que nos interesan para calcular, cualquier nivel.. de cualquier tamaño de tanque.

• L : Longitud ó Largo del Tanque
• r : Radio
• h : Altura del Nivel de Diesel

5. Comentario 3

Hola desarrollé la fórmula de Abel y quedó:

v = L·(2·r²·π·ASIN((H - r²)/r) + π·(2·(H - r)·(H·(2·r - H))^½ + r²·π))/(2·π)

impresionante.

Ahora aqui les dejo la formula para un tanque elíptico:

v = L·(a·b·ACOS(1 - H/b) + a/b·(H - b)·(H·(2·b - H))^½)

Sirve para el cilíndrico.

donde:

• L : longitud del tanque
• H : altura del líquido (0 <= H <= 2b)
• 2a : longitud del eje mayor
• 2b : longitud del eje menor ("H" se mide sobre este eje)

NOTA:

1. La función ACOS debe brindar valores de ángulo en radianes.
2. Es sencillo verificar que con H = 0 (tanque vacío), H = b (medio tanque lleno) ó H = 2b (tanque lleno) la fórmula satisface los resultados esperados (0, L·π·a·b/2 y L·π·a·b respectivamente).
3. La fórmula es la que se utiliza -habitualmente- en tanques horizontales de combustible en los que la variable suele ser H, esto es: la altura del líquido (la parte "mojada" de la vara testigo).
4. Si a, b, H y L están en metros entonces Volumen estará en m³.

6. Licencia

Este es un documento libre.

Autores: Daniel Ajoy, Mario Rodriguez Riotorto, Abel Castro, Gustavo

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.

7. Preguntas, Dudas, Comentarios, Peticiones

8. Enlaces

---