El valor de PI
Contenido
2. Historia
3. Cálculo de pi, método 1
4. Cálculo de pi, método 2
5. Un millón de cifras de pi
6. Licencia
7. Preguntas, Dudas, Comentarios, Peticiones
8. Enlaces
1. Introducción
Este artículo utiliza el lenguaje de programación Logo y el intérprete FMSLogo para calcular el valor de pi. Pi es una constante numérica que ya es parte del lenguaje de programación Logo y que se utiliza en la vida cotidiana para hacer cálculos relacionados con círculos, como diámetros, perímetros, radios. La constante pi también aparece en cálculos estadísticos o en integración de funciones trigonométricas, por lo que también es usada en programas informáticos que ayudan a resolver este tipo de problemas.
2. Historia
A medida que el diámetro de un círculo aumenta la longitud de su circunferencia aumenta también:
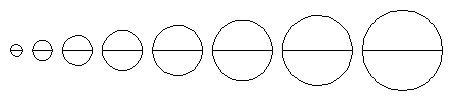
En la antigüedad se pensó que la fórmula para calcular la longitud de la circunferencia de un círculo, sabiendo su diámetro debería ser:
circunferencia = diámetro × π
El símbolo π representa un valor constante y se lo llama pi, pero no se sabía el valor de pi con exactitud. En la Biblia (1 Reyes 7, 23) dice que "Heriam"...
Hizo también una fuente circular de metal fundido, que medía cuatro metros y medio de diámetro y dos metros con veinticinco centímetros de alto. Su circunferencia, medida a cordel, era de trece metros y medio.
Es decir:
- circunferencia = diámetro × π
- 13.5 = 4.5 × π
¿Qué número multiplicado por 4.5 nos da 13.5? La respuesta es 3.
- 13.5 = 4.5 × π
- 13.5 = 4.5 × 3
π = 3
Para Heriam, el valor de pi era 3. En otros tiempos se pensaba que el valor de pi era otro:
Matemático o Lugar | año | valor |
La Biblia (1 Reyes 7, 23) | 3 | |
Papiro de Ahmes (Egipto) | 1650 a.C. | 3.16 |
Tablilla de Susa (Babilonia) | 1600 a.C. | 3.125 |
Bandhayana (India) | 500 a.C. | 3.09 |
Arquímedes de Siracusa | (287-212 a.C) | entre 223/71 y 220/70 |
Liu Hui (China) | 260 | 3.1416 |
Tsu Chung Chih | 480 | Entre : 3.145926 y 3.1415927 |
Al-Kashi (Persia) | 1429 | 3.1415926535897932 |
Franciscus Vieta (Francia) | (1540-1603) | 3.1415926536 |
3. Cálculo de pi, método 1
Una forma de calcular el valor de pi es calcular el perímetro de un polígono de muchos lados que está dentro de un círculo de diámetro conocido ya que mientras más lados tenga un polígono, más se parece a la circunferencia, y su perímetro se parecerá más a la longitud de la circunferencia:
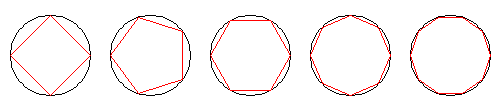
Podemos usar la computadora y LOGO para calcular el perímetro. El procedimento aproximación calcula el perímetro de un polígono de n lados. Mide la longitud de cada lado y va acumulando el valor en la variable perimetro:
para aproximación :n
ponpos [0 0]
avanza 100
haz "punto1 pos
haz "perimetro 0
repite :n [
ponpos [0 0]
giraderecha 360 / :n
avanza 100
haz "punto2 pos
haz "lado distancia :punto1
ponpos :punto1
haz "punto1 :punto2
haz "perimetro :perimetro + :lado
escribe frase "perimetro: :perimetro
]
fin
aproximación 6

Ya que el perímetro del hexágono es el valor aproximado de la longitud de la circunferencia, el valor aproximado de pi será:
- π = circunferencia / diámetro
- π = 599.999997189032 / 200
- π = 2.99999998594516
aproximación 8
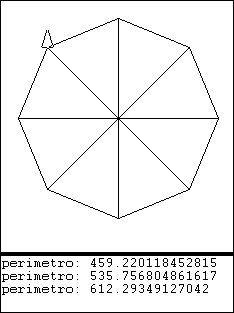
- π = 612.29349127042 / 200
- π = 3.0614674563521
aproximación 10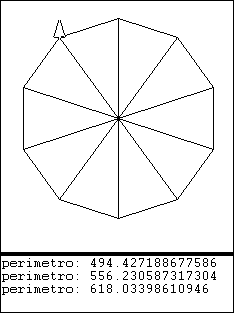
- π = 618.033985727494 / 200
- π = 3.09016992863747
aproximación 20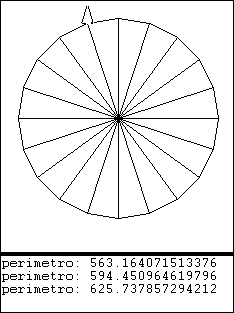
- π = 625.737857100848 / 200
- π = 3.12868928550424
aproximación 50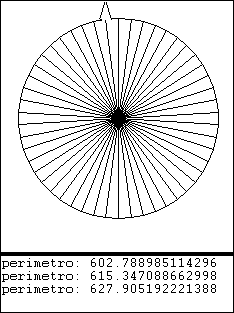
- π = 627.905192080941 / 200
- π = 3.13952596040471
A continuación están las aproximaciones al valor de pi usando polígonos de más lados. La última usando un polígono de 5000 lados:
lados: 100 lado: 6.28215088963844 perímetro: 628.215178348788 pi: 3.14107589174394
lados: 1325 lado: 0.474201334482517 perímetro: 628.317938052986 pi: 3.14158969026493
lados: 2550 lado: 0.246399187533157 perímetro: 628.318367865025 pi: 3.14159183932513
lados: 3775 lado: 0.166441058041578 perímetro: 628.318454217797 pi: 3.14159227108898
lados: 5000 lado: 0.125663024832287 perímetro: 628.318485386465 pi: 3.14159242693232
4. Cálculo de pi, método 2
Otro método que podría usarse para calcular el valor de pi se basa en la fórmula de la superficie del círculo:
- superficie = radio2 × π
- π = superficie / radio2
De esta forma podríamos saber el valor de pi si conociéramos el radio y la superficie de un círculo. Podemos estimar la superficie de un círculo que tiene un radio dado usando nuevamente la computadora y Logo. La idea es ubicar muchos puntos al azar dentro de un cuadrado. Imaginaremos que este cuadrado limita a un círculo que está dentro de él. Este círculo imaginario tendrá un radio que mide la mitad del lado del cuadrado. Cualquier punto que ubiquemos dentro del cuadrado y que esté más cerca del centro del círculo que su radio estará dentro del círculo imaginario y lo marcaremos con verde. Mientras que los puntos que estén fuera del círculo imaginario los marcaremos con rojo.
Luego podremos hacer la siguiente regla de tres: la cantidad de puntos verdes es al total de puntos dibujados como la superficie del círculo es a la superficie del cuadrado. Y podremos calcular la superficie del círculo con la siguiente fórmula:
superficie.círculo = puntos.verdes × superficie.cuadrado / total.puntos
para aproximación2 :total.puntos
borrapantalla ocultatortuga
haz "puntos.verdes 0
haz "lado 200
haz "radio :lado / 2
repite :total.puntos [
subelapiz ponxy azar :lado azar :lado
sisino :radio > distancia [100 100] [
poncolorlapiz 2
haz "puntos.verdes :puntos.verdes + 1
] [
poncolorlapiz 4
]
bajalapiz avanza 1
]
haz "superficie.cuadrado :lado * :lado
haz "superficie.círculo :puntos.verdes * :superficie.cuadrado / :total.puntos
escribe frase [superficie aprox:] :superficie.círculo
escribe frase [pi aprox:] :superficie.círculo / (:radio * :radio)
fin
aproximación2 1000
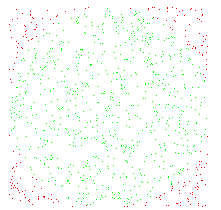
superficie aprox: 31440
pi aprox: 3.144
aproximación2 10000
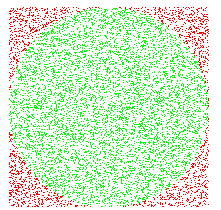
superficie aprox: 31636
pi aprox: 3.1636
aproximación2 100000

superficie aprox: 31481.2
pi aprox: 3.14812
5. Un millón de cifras de pi
El valor de pi no puede calcularse numéricamente con total precisión porque es un número irracional. Eso quiere decir que, por más cifras decimales que logremos calcular correctamente, siempre habrá más cifras decimales que desconocemos. En la actualidad se conocen miles de millones de cifras decimales del valor de pi. Este archivo contiene el primer millón de cifras de pi (1.3MB).
6. Licencia
Este es un documento libre.
Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.

