Graficador de Funciones

Creación de un Programa simple para Graficar Ecuaciones, y utilización de este programa para estimar la ubicación de las soluciones de sistemas no lineales de dos ecuaciones y dos incógnitas. Usando el lenguaje de programación Logo (Intérprete UCBLogo con LogoES)

Contenido

1. Una Ecuación

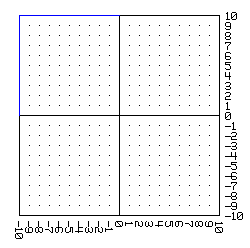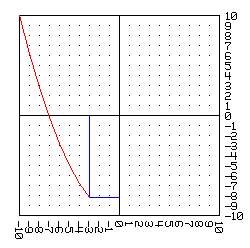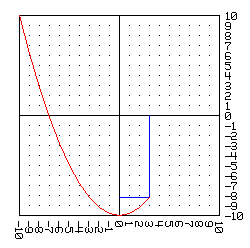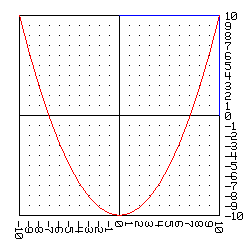
La técnica usual para graficar una ecuación de dos variables (x e y por ejemplo) consiste en poner la ecuación como y = f(x) de tal forma que al elegir unos valores de x podamos calcular los correspondientes valores de y. Así, para graficar:

y - 0.2 x² = -10

ponemos la ecuación como y = f(x), es decir despejamos la y:

y = 0.2 x² - 10

luego, elegimos unos valores para x, digamos:

-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10

y obtenemos los correspondientes valores de y. Como resultado de este proceso obtenemos un conjunto de pares, o puntos, qué, si los ubicamos en el plano cartesiano uno a uno en orden, y vamos trazando segmentos de rectas entre ellos, obtenemos una aproximación de la representación gráfica de la ecuación planteada:

y = 0.2 · -10 · -10 - 10 =  10.0 --> ( -10 ,  10.0 ) y = 0.2 ·  -9 ·  -9 - 10 =   6.2 --> (  -9 ,   6.2 ) y = 0.2 ·  -8 ·  -8 - 10 =   2.8 --> (  -8 ,   2.8 ) y = 0.2 ·  -7 ·  -7 - 10 =  -0.2 --> (  -7 ,  -0.2 ) y = 0.2 ·  -6 ·  -6 - 10 =  -2.8 --> (  -6 ,  -2.8 ) y = 0.2 ·  -5 ·  -5 - 10 =  -5.0 --> (  -5 ,  -5.0 ) y = 0.2 ·  -4 ·  -4 - 10 =  -6.8 --> (  -4 ,  -6.8 ) y = 0.2 ·  -3 ·  -3 - 10 =  -8.2 --> (  -3 ,  -8.2 ) y = 0.2 ·  -2 ·  -2 - 10 =  -9.2 --> (  -2 ,  -9.2 ) y = 0.2 ·  -1 ·  -1 - 10 =  -9.8 --> (  -1 ,  -9.8 ) y = 0.2 ·   0 ·   0 - 10 = -10.0 --> (   0 , -10.0 ) y = 0.2 ·   1 ·   1 - 10 =  -9.8 --> (   1 ,  -9.8 ) y = 0.2 ·   2 ·   2 - 10 =  -9.2 --> (   2 ,  -9.2 ) y = 0.2 ·   3 ·   3 - 10 =  -8.2 --> (   3 ,  -8.2 ) y = 0.2 ·   4 ·   4 - 10 =  -6.8 --> (   4 ,  -6.8 ) y = 0.2 ·   5 ·   5 - 10 =  -5.0 --> (   5 ,  -5.0 ) y = 0.2 ·   6 ·   6 - 10 =  -2.8 --> (   6 ,  -2.8 ) y = 0.2 ·   7 ·   7 - 10 =  -0.2 --> (   7 ,  -0.2 ) y = 0.2 ·   8 ·   8 - 10 =   2.8 --> (   8 ,   2.8 ) y = 0.2 ·   9 ·   9 - 10 =   6.2 --> (   9 ,   6.2 ) y = 0.2 ·  10 ·  10 - 10 =  10.0 --> (  10 ,  10.0 )

• y - 0.2 x² = -10
• (2.8) - 0.2 (8)² = -10
• (2.8) - 0.2 (64) = -10
• (2.8) - 12.8 = -10
• (2.8) - 12.8 = -10
• -10 = -10

Sin embargo, las coordenadas del punto (7,1), no cumplen con la ecuación:

• (1) - 0.2 (7)² =?= -10
• (1) - 0.2 (49) =?= -10
• (1) - 9.8 =?= -10
• -8.8 =?= -10
• -8.8 > -10

En este caso el lado izquierdo de la ecuación es mayor que el lado derecho de la ecuación. Por otro lado, las coordenadas del punto (8,1), tampoco cumplen con la ecuación:

• (1) - 0.2 (8)² =?= -10
• (1) - 0.2 (64) =?= -10
• (1) - 12.8 =?= -10
• -11.8 =?= -10
• -11.8 < -10

Lo que ocurrió en esta ocasión es que el lado izquierdo de la ecuación es menor que el lado derecho de la ecuación.

Si dentro de un área cuadrada escogemos regularmente muchos punto y vemos si el lado izquierdo es mayor o menor que el lado derecho de la ecuación; y, dependiendo de si pasa lo uno o lo otro, coloreamos estos puntos de dos colores distintos el gráfico que resulta podría ser:

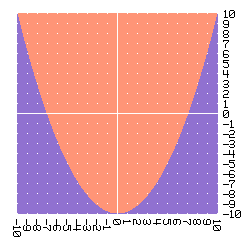
En este gráfico resultó que, en el borde donde el área de un color se vuelve de otro color, es donde el lado izquierdo de la ecuación es igual al lado derecho de la ecuación. Es decir, el borde de las regiones representa los puntos que cumplen la ecuación.

Esta forma de graficar ecuaciones tiene la ventaja que no es necesario representar las ecuaciones en forma de función, se pueden graficar funciones implícitas y explícitas. Es más, no es necesario que las funciones asociadas a las ecuaciones sean continuas, ni siquiera es necesario que sean funciones.

Por ejemplo, sabemos que la función asociada a la ecuación xy = 1 es y = 1/x que es discontinua, es decir que para dibujarla hay que levantar el lápiz. Dicho de otro modo, no podemos esperar un valor de y para x=0, porque la división para 0 no está definida.

Sin embargo, usando este otro método el problema desaparece y la gráfica luce así:

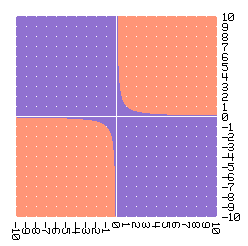
Para ejemplificar que para graficar no es necesario despejar una función a partir de la ecuación usemos la ecuación de un círculo: x² + y² = 36.

La graficamos implícitamente.

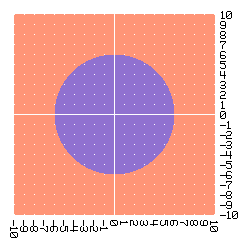
Para producir la gráfica de un círculo de la manera usual tendríamos que extraer dos funciones de la ecuación del círculo:

1. y = RaizCuadrada (36 - x²)
2. y = -RaizCuadrada (36 - x²)

graficar una función, y luego graficar la otra función, pero siempre teniendo en cuenta que no podremos pedir valores de y para valores de x>6, porque luego no podríamos sacar la raíz cuadrada de valores negativos. Aún así, se trata solamente de dos funciones. La ecuación cos(2x) = cos(y) tiene asociada un número infinito de funciones:

Es decir, con el método usual hay que prestar atención a varios detalles que dependen de las particularidades de cada ecuación.

El método de las áreas coloreadas es más general y más sencillo, pero sólo se hace posible porque las computadoras son muy rápidas y pueden determinar el color de muchos puntos en poco tiempo. En estos ejemplos hemos estado calculando el color de 201x201 = 40401 puntos. La computadora lo hace en pocos segundos.

2. Dos Ecuaciones

El procedimiento que hemos estado usando para determinar de qué color pintar cada punto es el siguiente. Recibe dos entradas: las expresiones del lado izquierdo y del lado derecho de la ecuación. Devuelve -1 si el lado izquierdo es mayor, 1 si el lado derecho es mayor, y 0 si ambos lados son iguales. Por ejemplo:

Si una ves escogido el par (x,y) el procedimiento iguales nos devuelve 1, el color escogido será rojo claro (código 12), si devuelve 0 será gris (código 15), si devuelve -1 será azúl claro (código 13). Esto se puede hacer fácilmento definiendo un arreglo colores así:

Los colores de los extremos del arreglo: rojo intenso (código 1) y azúl intenso (código 4), los reservamos para la siguiente parte del proyecto.

Pensamos que es posible graficar dos ecuaciones simultáneamente para observar dónde se cruzan las curvas de ambas. Los puntos en donde ocurran estos cruces serán las soluciones de aquel par de ecuaciones. Usemos el ejemplo típico del sistema lineal de dos ecuaciones y dos incógnitas, ambas ecuaciones son rectas:

• 15y = -4x + 50
• 15y = 8x - 10

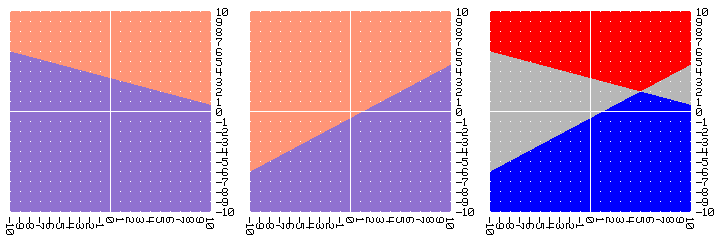
El punto (5,2) parece ser solución. Y efectivamente:

• 15 (2) = -4 (5) + 50
• 15 (2) = 8 (5) - 10

• 30 = -20 + 50
• 30 = 40 - 10

• 30 = 30
• 30 = 30

Es fácil ver que, al sumar los dos primeros gráficos, en el área donde se juntan las áreas rojas, el rojo se intensifica (1 + 1 = 2), en el área donde se juntan las áreas azúles, el azúl se intensifica (-1 + -1 = -2), y en las áreas donde se juntan rojo y ázul, los colores se anulan y quedan grises (-1 + 1 = 1 + -1 = 0).

En este nuevo ejemplo, el sistema de ecuaciones representa la intersección de dos parábolas. Los puntos de intersección parecen ser (-1,3) y (4,8).

• y = 4x - x² + 8
• y = x² - 2x

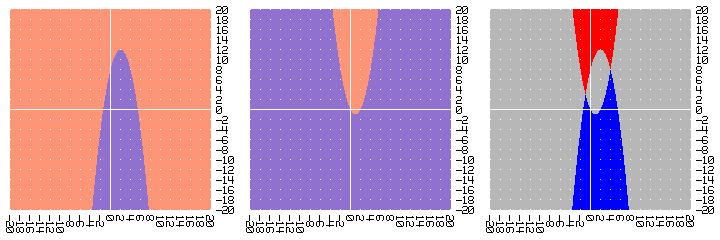
Y efectivamente:

(-1,3)	(4,8)
3 = 4 (-1) - (-1)2 + 8 3 = (-1)2 - 2 (-1) 3 = -4 - 1 + 8 3 = 1 - (-2) 3 = 8 - 5 = 3 3 = 1 + 2 = 3	8 = 4 (4) - (4)2 + 8 8 = (4)2 - 2 (4) 8 = 16 - 16 + 8 8 = 16 - 8 8 = 0 + 8 = 8 8 = 8

Lo siguiente representa los cuatro puntos de intersección entre una elipse oblicua y una parte de una hipérbola:

• 2y² = 4x - xy + 30
• 30 = x² + y² + 1.3 xy

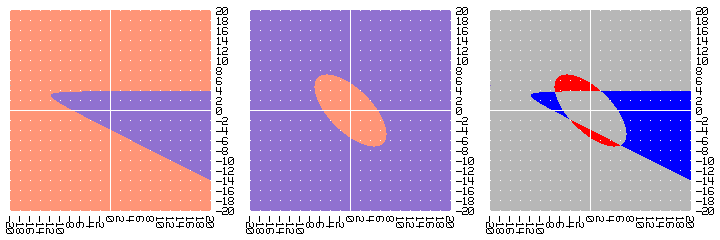
Y lo siguiente representa los tres puntos de intersección entre una curva elíptica y las dos partes de una hipérbola:

• y² = x³ - x
• 4xy=1

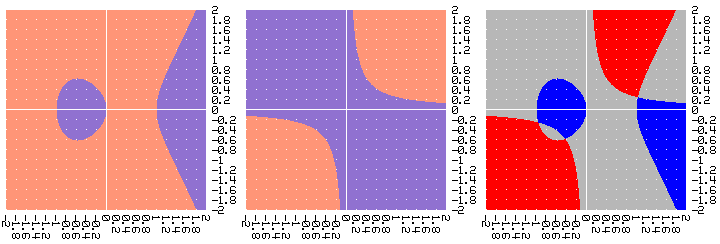
3. El Programa

El procedimiento que hemos estado utilizando para realizar estos gráficos es el siguiente:

El procedimiento cuadricula recibe tres entradas: las dos ecuaciones y el tamaño de la cuadrícula.

El primer bloque de instrucciones, usadas para dibujar los puntos coloreados, significa: Varía los valores de x e y desde menos tamaño hasta más tamaño (por ejemplo, desde -10 hasta 10). Hazlo sistemáticamente y en pasos pequeños (por ejemplo, en pasos de 10/100 = 0.1 unidades). Luego, colócate en la coordenada de la pantalla adecuada, calculada a partir de los valores de x e y. Calcula el color con que vas a pintar el punto, utilizando para esto la suma de los resultados del procedimiento iguales, aplicado a cada una de las dos ecuaciones. Finalmente, dibuja un punto.

El segundo bloque de instrucciones, usadas para dibujar los puntos guías, significa: Usando color blanco (código 7), para cada valor entre -100 y 100 saltando de 10 en 10, tanto de x como de y, colócate en coordenadas (x,y) y dibuja un punto.

El tercer bloque de instrucciones, usadas para dibujar los ejes, significa: Colócate en la coordenada de la pantalla (-100,0) y, con el lápiz abajo, muévete hasta la coordenada (100,0). Es decir, traza una raya entre esas dos coordenadas. Luego, traza también una raya entre las coordenadas (0,-100) y (0,100).

El cuarto bloque de instrucciones, usadas para dibujar los números, significa: Por todos los valores de i entre -100 y 100 saltando de 10 en 10, colócate en la parte inferior de la gráfica y rotula en número adecuado. Luego colócate en la parte derecha de la gráfica y rotula el mismo número. Los números de la parte inferior deben ser dibujados con una orientación (rumbo) diferente que los números de la parte derecha de la gráfica.

4. Epílogo

El objetivo final de este artículo es mostrar cómo en la escuela el tratamiento de la solución de sistemas de dos ecuaciones y dos incógnitas se segmenta en diferentes tópicos inconexos (debido a las dificultades para abordarlos algebraícamente): primero se distinguen los sistemas lineales, casi al final del colegio se abordan las cónicas, y en la universidad rara vez se ven gráficas de curvas elípticas.

Una computadora y un programa de 20 líneas pueden ayudar a juntar estos contenidos nuevamente y al mismo tiempo ayudar a mostrar una vista panorámica del asunto.

5. Licencia

Este es un documento libre.

Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.

6. Preguntas, Dudas, Comentarios, Peticiones

7. Enlaces

---