Superficie de un triángulo

LogoFE es Logo Functional Extensions, una librería de procedimientos para ser usados con MSWLogo o con UCBLogo. El objetivo de LogoFE es proporcionar un gran "caja de herramientas" para la construcción de pequeños programas útiles o para explorar temáticas de Matemáticas, Física, Química, Estadística y otras materias de escuela, colegio y universidad.

Contenido

1. Determinante de una Matriz

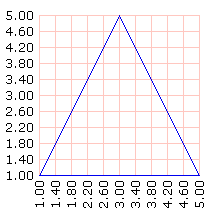
Cálculo del superficie de un triángulo dado por sus coordenadas:

Con LogoFE, podemos dibujar tal triángulo así:

bp graflineas [] trans [[1 1] [5 1] [3 5] [1 1]]

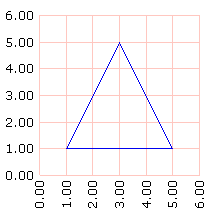
O con algunos refinamientos, así:

bp graflineas [  [Ytic: natural]  [Xtic: natural]  [XMax: 6] [XMin: 0]  [YMax: 6] [YMin: 0] ] trans [[1 1] [5 1] [3 5] [1 1]]

Es fácil ver que tiene 4 unidades de altura por 4 unidades de base, así que su superficie debe ser S = 4 * 4 / 2 = 8

Sin embargo, un método para determinar la superficie de un triángulo dadas las coordenadas de sus puntos es usando un determinante.

Como se explica aquí, por ejemplo: Area de un triangulo

Para lo cual también podemos usar LogoFE:

Tenemos las coordenadas de los tres puntos:

En este punto tenemos ya los elementos de nuestro determinante:

Calculamos el determinante:

Y dividimos para 2:

A esta función la llamaremos super_triangulo:

Pero Carlos mencionó algo acerca de que a veces la superficie sale negativa cuando las coordenadas de los puntos son dadas en un orden diferente.

Cuáles son esos posibles ordenamientos:

Y para cuáles de esos ordenamientos la superficie es negativa:

Así que mejor será que la función super_triangulo sea modificada así:

2. División de Números Complejos

Otra forma de calcular la superficie de un triángulo (números complejos)

El plan es:

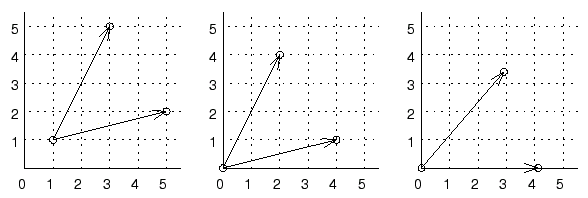
1. Conceptualizar los 3 puntos como números complejos.
2. Restar dos de ellos del tercero, y trabajar con los números complejos resultantes (segunda figura)
3. Rotar los dos números de tal manera que uno de ellos quede sobre el eje X (parte real).
4. La superficie del triángulo es la parte real del número complejo que quedó totalmente sobre el eje X, multiplicada por la parte compleja del otro número (la altura del triángulo), y esto dividido para 2.

Estos son los números complejos (coordenadas de los tres puntos del triángulo)

Separo el último:

Distribuyo el último entre los otros:

Distribuyo y resto:

Al primer número lo llamaremos C y al otro lo llamaremos D.

La multiplicación de complejos es equivalente a una rotación. Lo siguiente es para determinar un número (complejo) tal que al multiplicarlo por los dos números anteriores haga que el primero de ellos (C) quede totalmente en el plano real. Trabajaremos con C:

El valor absoluto (la magnitud) de C es:

Queremos que toda esa magnitud quede en el eje x (eje real) la parte imaginaria debe ser 0.

Para encontrar un número N tal que al multiplicarlo por C nos de éste último número [4.12310562561766 0] (llamémoslo R) despejamos:

Nos preparamos para calcular N haciendo la división de complejos:

Necesitaremos este paso intermedio luego:

A continuación tenemos N y D:

N por D nos da el vector D rotado tal como aparece en la última figura:

Su parte compleja es:

Esa es la altura del triángulo. La base del triángulo ya la habíamos calculado es:

Recolectándo ambos resultados:

Y multiplicándolos obtenemos (base por altura):

base por altura sobre 2:

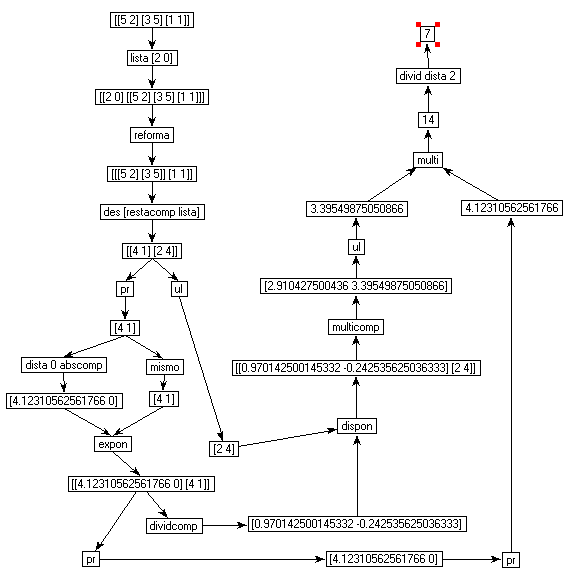
A continuación un diagrama que describe más o menos como los datos de entrada van fluyendo por las funciones hasta producir las salidas:

3. Producto Cruz

Hemos visto dos métodos para determinar la superficie de un triángulo dado por las coordenadas de sus tres vértices:

1. construyendo un determinante y resolviéndolo.
2. utilizando aritmética de números complejos.

Ahora presentaré una tercera forma: Utilizando el producto "cruz".

El resultado de aplicar el producto "cruz" a dos vectores es un vector con dirección perpendicular a plano formado por los dos vectores y de magnitud igual a la superficie de paralelogramo formado por ellos.

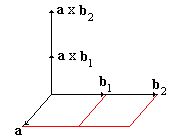
La estrategia es la siguiente:

1. Restar de dos pares coordenados (vectores), el tercero
2. Calcular el producto cruz de los vectores
3. El vector resultante sólo tendrá su componente en el eje Z diferente de 0. porque será perpendicular al plano XY, porque los dos vectores multiplicados pertenecen a este plano. El valor de esta componente dividido para 2 es la superficie del triángulo que nos interesa.

Cálculo del área de un triángulo dado por sus coordenadas:

Separo el primer par coordenado:

Lo distribuyo entre los otros dos:

Hago sendas restas:

Convierto los vectores en tridimensionales añadiendo un 0 como componente Z de cada uno:

Aplico el producto "cruz":

La componente Z es la que nos interesa:

La dividimos para 2:

Llamamos a nuestro programa "super2_triangulo":

Utilizamos nuestro programa:

4. Producto Punto

José Carrión Beltrán nos dice:

Intentemos nuevamente con los puntos utilizados para la solución con números complejos:

Separo el último:

Distribuyo el último entre los otros:

Hasta aquí todo igual, pero ahora hagamos la resta en forma diferente.

Distribuyo y resto vectores:

Porque transpon [diferencia] es resta de vectores:

Luego giremos uno de los vectores 90 grados:

Luego, valor absoluto de la mitad del producto punto de lo anterior:

5. Licencia

Este es un documento libre.

Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.

6. Preguntas, Dudas, Comentarios, Peticiones

7. Enlaces

---