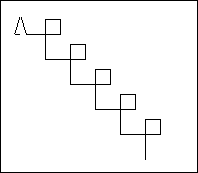Matemáticas para Niños
De: Teaching Children to be Mathematicians vs. Teaching Them About Mathematics
Logo Memo No. 4 / July 1971
Massachusets Institute of Technology / A.I. Laboratory
Seymour Papert
Contenido
2. Geometría de Tortuga: Una parte amable y compresible de las matemáticas
3. Cuáles son los Conceptos Primarios de las Matemáticas
4. Preguntas, Dudas, Comentarios, Peticiones
5. Enlaces
1. Prefacio
La definición de que "ser un matemático" es saber un conjunto de hechos matemáticos, es tan mala como la definición de que "ser un poeta" es conocer un conjunto de hechos lingüísticos. Algunos reformistas modernos de educación matemática darán a esta sentencia un asentimiento demasiado fácil y comentarán: "Si, ellos deben comprender, no solamente saber". Pero esto pasa por encima el punto fundamental que "ser un matemático", como "ser un poeta", o un compositor, o un ingeniero, significa hacer, en lugar de conocer o comprender. Este ensayo es un intento de explorar algunas maneras en las cuales uno podría ser capaz de poner a los niños en una mejor posición para hacer matemáticas en lugar de meramente aprender sobre ellas
...
Se asume generalmente en nuestra sociedad que todo niño debe, y puede, tener experiencias de trabajo creativo en lenguaje y artes plásticas. Es igualmente asumido en forma general que muy pocas personas pueden trabajar creativamente en matemáticas. Yo creo que ha existido una conspiración involuntaria por parte de psicólogos y matemáticos de mantener esta suposición. Los psicólogos contribuyen a esta por ignorancia genuina sobre cómo podría ser una expresión de trabajo matemático creativo. Los matemáticos, muy frecuentemente, lo hacen por elitismo, en la forma de una convicción profunda de que la creatividad matemática es el privilegio de una minúscula minoría.
Nuevamente aquí, es necesario, si deseamos claridad, protegernos contra un asentimiento facilista de los reformistas de la educación de matemáticas que dicen "Sí, por esto debemos usar el Método de Descubrimiento". Ya que, cuando "Descubrimiento" significa descubrimiento esto es fantástico, pero en la práctica "Descubrimiento" comúnmente significa algo similar a seguir la siguiente fantasía acerca de una clase de poesía: el maestro que usa el método de descubrimiento ha perfeccionado una serie de preguntas que llevan a la clase a descubrir la línea "Del cielo cayó una rosa". Mi punto no es, si es esto es bueno o malo, sino que nadie lo confundiría con trabajo poético creativo.
¿Es posible para los niños hacer matemáticas creativas (es decir: hacer matemáticas) en todas y cada una de las etapas de su vida estudiantil? Yo argumentaré que la respuesta es: sí, pero una gran cantidad de trabajo matemático creativo realizado por matemáticos adultos es necesario para hacerlo posible. La razón de la inclusión de esta salvedad es que las ramas tradicionales de las matemáticas no ofrecen el campo más fértil para el crecimiento fácil y prolífico de los rasgos matemáticos de la mente. Quizá debamos desarrollar ramas un tanto nuevas de las matemáticas con la propiedad especial de que ofrezca a los novatos más espacio para juguetear creativamente, que lo que ofrece la teoría de los números o el álgebra moderna. En las siguientes páginas se encontrarán ejemplos específicos de lo que pretenciosamente podría llamarse "nuevas ramas de las matemáticas orientadas pedagógicamente" pero que podrán sugerir al lector cooperativo lo que esta frase podría significar.
Los lectores quisquillosos no tendrán problemas en encontrar objeciones. Los elitistas matemáticos dirán: "Cómo se atreve a traer estas trivialidades a perturbar nuestra contemplación de las estructuras matemáticas verdaderas". La gente práctica dirá: "¿Jugueteos y ostentaciones? (Romping? Pomping?) ¿Quién lo necesita? ¿Y qué hay de las habilidades prácticas en aritmética?"
El elitista y el práctico están expresando la misma objeción en palabras diferentes. Permítanme decirlo de otra manera, "Las escuelas tradicionales se han encontrado con que las matemáticas son difíciles de enseñar al, así llamado, niño promedio. Alguien presenta un nuevo conjunto de actividades, que parecen ser divertidas y fáciles de aprender. ¡El declara que esto es Matemáticas! Bueno, eso no las convierte en Matemáticas, y no las convierte en soluciones para ninguno de los graves problemas que enfrenta el mundo de la educación de matemáticas".
Este argumento saca a relucir cuestiones serias, de entre las cuales yo identificaré una cuestión que plantearé de algunas formas diferentes:
Al hacerse uno matemático, ¿aprende algo más, y más general, que el contenido específico de los tópicos matemáticos particulares? ¿Existe una tal cosa llamada la Forma de Pensar Matemática ? Una vez que uno la ha adquirido, ¿se vuelve más fácil aprender tópicos particulares, como aquellos que obsesionan a los críticos elitistas y prácticos?
Los psicólogos a veces reaccionan diciendo, "Ah ya, usted ser refiere al problema de la transferencia". Pero yo no me refiero a nada análogo a experimentos sobre si los estudiantes a los que se les enseñó álgebra el año pasado automáticamente aprenden geometría más fácilmente que los estudiantes que usaron su tiempo el año pasado haciendo gimnasia. Mi pregunta es si se puede identificar y enseñar (o fomentar el crecimiento de) algo a parte de álgebra o geometría. Si duda, esta otra cosa (llamémosla FPM) solamente puede ser enseñada usando tópicos particulares como vehículos. Pero el experimento de la "transferencia" se cambia fundamentalmente si la pregunta es si uno puede usar el álgebra como un vehículo para enseñar deliberadamente conceptos y aptitudes generales y transferibles . La conjetura que subyace este ensayo es una muy reservada respuesta afirmativa a esta pregunta. Sí, uno puede usar el álgebra como un vehículo para iniciar a los estudiantes en la forma matemática de pensar . Pero para hacerlo efectivamente se deben identificar tantos componentes como sean posibles de las aptitudes generales que se intentan enseñar; cuando esto se haya hecho, nos parecerá que el álgebra (en el sentido tradicional) no era un vehículo particularmente bueno.
Todas las opciones alternativas para el vehículo descrito arriba involucran el uso de computadores, pero de una manera que es diferente a las sugerencias usuales que usarlos como "máquinas de enseñar" o como "super-reglas de cálculo". En nuestro ideal de un laboratorio matemático para la escuela, el computador es usado como un medio para controlar procesos físicos con el propósito de lograr objetivos definidos ... Para alcanzar estos objetivos se necesitarán principios matemáticos; de manera inversa, en este contexto los principios matemáticos se convierten en fuentes de poder, y de esta manera estos principios adquieren significado para los grandes grupos de estudiantes que no logran encontrar ningún sentido o gusto en las matemáticas de los libros y quienes, bajo las condiciones imperantes de la escuela, simplemente se apartan, etiquetándose a si mismos como "sin inclinaciones por las matemáticas".
La aceptación facilista de esto es de la forma: "Sí, las aplicaciones son motivadoras". Pero "motivación" no logra distinguir entre: trabajo extraño al estudiante, de trabajo en el que el estudiante de involucra personalmente y obtiene recompensas materiales o sociales. Para desarrollar este punto necesito separar algunos aspectos de la forma cómo un niño se relaciona con su trabajo.
Uno, simple e importante, es la escala de tiempo. El niño interesado en volar un modelo de avión bajo control de un computador trabajará en su proyecto por un período de tiempo largo. Tendrá tiempo para intentar diferentes estrategias para abordar sub-problemas. Tendrá tiempo para hablar sobre ello, para relacionarlo con otros intereses y problemas. Este enfoque orientado a proyectos contrasta con el enfoque de uso de problemas usado por la mayoría de maestros de matemáticas: una mala característica del problema típico es que el niño no se queda con él por suficiente tiempo para beneficiarse mucho ya sea del éxito o el fracaso.
Junto con la escala de tiempo viene la estructura. Un proyecto es suficientemente largo como para tener fases reconocibles, tales como planeación, escoger la estrategia de intentar un caso muy simple al principio, encontrar la solución simple, depurarla, y así. Y si la escala de tiempo es suficientemente larga, y la estructura suficientemente clara, el niño puede desarrollar un vocabulario para articular una discusión sobre le proceso de trabajar hacia sus objetivos.
Yo creo en la discusión articulada (en monólogo o diálogo) de cómo un resuelve los problemas, de porqué uno metió la pata en esto o aquello, de qué brechas o deformaciones existen en el conocimiento propio y de qué se podría hacer al respecto. Yo defenderé esta creencia contra dos objeciones distintas. Una objeción dice: "es imposible verbalizar; los problemas se resuelven por actos intuitivos de compresión y estos no pueden ser articulados". La otra objeción dice: "Es malo verbalizar; recuerde el ciempiés que se paralizó cuando la rana le preguntó qué pierna iba delante de cuál".
Se debe prestar atención a los errores de cuantificadores cuando se discuten estas objeciones. Por ejemplo, J. S. Bruner nos dice (en su libro "Towards a Theory of Instruction") que el considera a las palabras y a los diagramas "impotentes" para hacer que un niño logre manejar una bicicleta. Pero, mientras su evidencia muestra (en el mejor de los casos) que algunas palabras y diagramas son impotentes, él sugiere la conclusión que todas las palabras y diagramas son impotentes. La conjetura interesante es esta: la impotencia de las palabras y los diagramas usados por Bruner se explica por los orígenes culturales de Bruner; el vocabulario y marco conceptual de la psicología clásica es simplemente inadecuado para la descripción de un proceso tan dinámico como el manejar una bicicleta! Para llevar la retórica un poco más allá, sospecho que si Bruner hubiese tratado de escribir un programa para hacer que una IBM 360 conduzca una motocicleta controlada por radio, hubiese concluido (para mantener la consistencia) que el código de instrucciones de la 360 era impotente para esta tarea. Ahora, en nuestro laboratorio hemos estudiado cómo la gente balancea bicicletas y aparatos más complicados tales como uniciclos o pelotas de circo. No hay nada complejo, misterioso o indescriptible acerca de estos procesos. Los podemos describir de una manera no-impotente con tal que un sistema descriptivo apropiado haya sido establecido con anterioridad. Los componentes clave del sistema descriptivo descansan en conceptos tales como: la idea de una teoría de "primer orden" o "lineal" en la cual se puede asumir que las variables de control actúan independientemente; o la idea de la retroalimentación.
Un problema fundamental de la teoría de la educación matemática es el de identificar y nombrar los conceptos necesarios para permitir al novato discutir su pensamiento matemático de una manera clara y articulada. Y cuando conocemos estos conceptos quizá queramos buscar (o inventar) áreas del desarrollo matemático que ejemplifiquen estos conceptos particularmente bien. La siguiente sección de este ensayo describe un nuevo pedazo de las matemáticas con la propiedad de que permite una discusión clara, y modelos simples, de heurísticas que son nebulosas o confusas para los novatos cuando se las presenta dentro del contexto de las matemáticas elementales más tradicionales.
2. Geometría de Tortuga: Una parte amable y compresible de las matemáticas
La tortuga es un juguete cibernético capaz de moverse hacia adelante y hacia atrás en una dirección particular (relativa a sí misma) o de rotar sobre su eje central. Tiene un lápiz , y la tortuga puede estar en dos estados BAJALAPIZ o SUBELAPIZ. La tortuga está construida para actuar tecleando comandos cuyos efectos se ilustran a continuación.
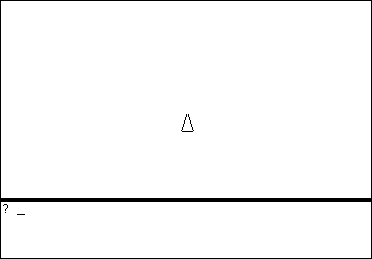
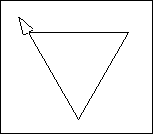
En todo instante la tortuga está en un lugar particular orientada en una dirección particular. El lugar y la dirección juntas son el estado geométrico de la tortuga. Las imágenes muestran a la tortuga en su campo, dibujado aquí sólo para dar al lector un marco de referencia:
La figura triangular muestra la dirección |
|
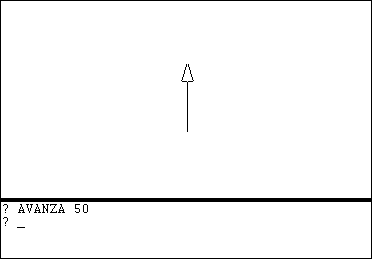
AVANZA 50 La tortuga avanza 50 unidades en la dirección en la que apunta. |
|
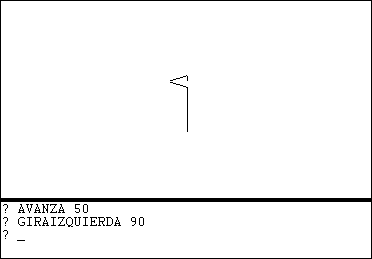
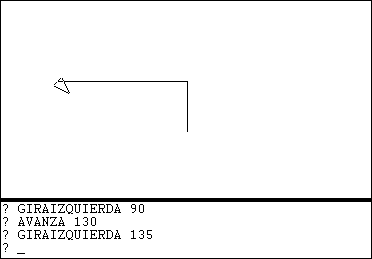
GIRAIZQUIERDA 90 La posición de la tortuga se mantiene fija. Rotó 90 grados hacia su izquierda. Por lo que su dirección cambió. |
|
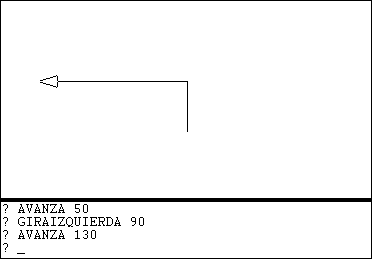
AVANZA 130 La tortuga avanzó 130 unidades en su nueva dirección. |
|
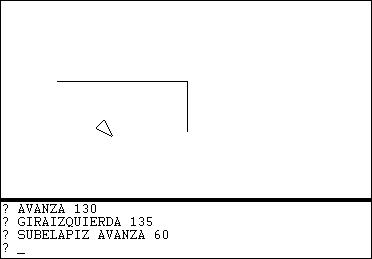
GIRAIZQUIERDA 135 La tortuga rotó a su izquierda 135 grados |
|
SUBELAPIZ AVANZA 60 SUBELAPIZ (No produce ningún efecto visible. Pero la siguiente instrucción AVANZA ya no dejará un rastro). El efecto de SUBELAPIZ es poner a la tortuga en un estado en el que no deja un rastro: el lápiz no dibuja en el campo. |
|
2.1. Comandos Directos
Los siguientes comandos hacen que la tortuga dibuje la figura que lo acompaña
BAJALAPIZ | |
2.2. Definición de procedimientos
Se supone que el computador aceptará comandos del lenguaje Logo (el cual ha sido expresamente desarrollado con el propósito de enseñar a los niños, no programación, sino matemáticas). La expresión para afirmar el hecho de que estamos listos para definir un procedimiento se ilustra con el siguiente ejemplo. Primero decidimos en nombre del procedimiento. Supongamos que lo llamamos PAZ. Luego escribimos:
PARA PAZ
AVANZA 100
GIRADERECHA 60
AVANZA 100
RETROCEDE 100
GIRAIZQUIERDA 120
AVANZA 100
FIN
Estas son indicaciones que le dicen al computador cómo realizar PAZ. La palabra PARA informa al computador que la siguiente palabra, PAZ, está siendo definida y que las líneas siguientes constituyen su definición.
La tortuga no se mueve mientras escribimos esto. La palabra PARA y los comandos siguientes indican que no le estamos diciendo que vaya hacia adelante y así; en lugar de eso le estamos diciendo cómo ejecutar el nuevo comando. Cuando indicamos con la palabra FIN* que nuestra definición está completa la máquina responde:
PAZ definido
y entonces podemos teclear:
BAJALAPIZ PAZ
La tortuga llevará a cabo los comandos y dibujará la figura anterior. Si en lugar de anteceder el nuevo comando PAZ con el comando BAJALAPIZ lo hiciéramos con el comando SUBELAPIZ la tortuga realizaría los movimientos pero no dejaría rastro visible.
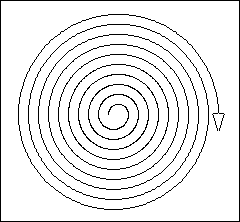
Al signo de la paz de la figura anterior le falta un círculo. Cómo podemos describir un círculo en el lenguaje de la tortuga?
Una idea que se presenta con facilidad a los matemáticos es: hagamos que la tortuga dg pequeños pasos hacia adelante y luego que gire un poquito y que se mantenga haciendo esto. Esto quizá no produzca un círculo, pero es un buen plan inicial, así que empecemos pongamos manos a la obra. Definamos el procedimiento:
PARA CIRCO
AVANZA 5
GIRADERECHA 7
CIRCO
FIN
Note ahora dos aspectos:
- El procedimiento se refiere a sí mismo en su última línea. Esto luce circular (aun cuando no en el sentido que requerimos) pero realmente no lo es. El efecto es meramente el de establecer un proceso sin fin al poner al computador en la espinosa situación en la que usted estaría si fuese una persona que no puede romper una promesa y se le hubiese engatusado para que diga: "Prometo repetir la frase que acabo de decir".
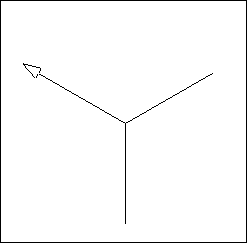
- Seleccionamos los números 5 y 7 porque parecían pequeños, pero sin una idea firme de qué es lo que pasaría. Sin embargo, una ventaja de tener un computador es que podemos poner a prueba nuestro procedimiento para ver lo que hace. Si se produce algún efecto no deseado siempre podemos depurarlo ; en este caso, quizá, seleccionado números diferentes. Si, por ejemplo, la tortuga dibujara algo como la figura de la izquierda, podríamos decirnos a nosotros mismos: "no está girando lo suficiente" y reemplazar un 7 por un 8; por otro lado, si dibujara la figura de la derecha podríamos reemplazar un 7 por un 6.
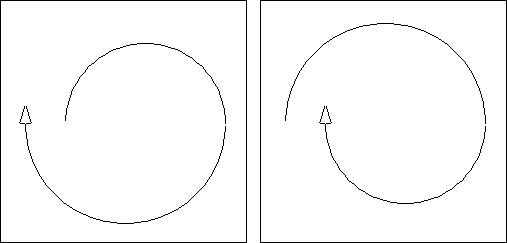
Me gustaría poder coleccionar estadísticas de cuántos lectores matemáticamente sofisticados cayeron en mi trampa! La experiencia demuestra que una gran porción de estudiantes licenciados en Matemáticas hubiesen caído. De hecho, el procedimiento no puede generar ninguna de las dos figuras! Si lo hiciera, sin duda produciría un espiral infinito. Y uno puede fácilmente ver que esto no es posible ya que la misma secuencia de comandos tendría que producir partes de curva que serían casi planas, y otras partes que fuesen muy curvadas. Más técnicamente, uno puede darse cuenta que el procedimiento CIRCOS debe producir una aproximación a un círculo (lo que es, para todos los propósitos prácticos, un círculo) porque debe producir una curva de curvatura constante.
Se podría llegar a la misma conclusión a partir de un teorema más general. A los procedimientos como CIRCO los llamamos procedimientos de instrucciones fijas porque no contienen variables.
Teorema: Cualquier figura generada por un procedimiento de instrucciones fijas pude ser limitado ya sea por un círculo o por dos líneas rectas paralelas.
Ejemplos de figuras que pueden y que no pueden ser limitadas de tal manera se muestran a continuación:
Una figura limitada por líneas paralelas
| Una figura que no puede ser limitada ni por líneas paralelas ni por un círculo
|
Ahora mostraremos cómo hacer procedimientos con entradas en el sentido de que el comando AVANZA tiene un número, llamado una entrada, asociado al comando. El siguiente ejemplo muestra cómo se hace esto. (Las palabras en la línea de título precedidas por ":" son los nombres de las entradas, en lugar de las x's usadas en el Álgebra escolar). En clases de quito grado solemos leer :NUMERO como puntos NUMERO o la cosa de NUMERO, para enfantizar que lo que de lo que se está tratando no es la palabra "NUMERO", sino la cosa que tiene como nombre la palabra "NUMERO".
PARA POLI :PASO :ANGULO
AVANZA :PASO
GIRAIZQUIERDA :ANGULO
POLI :PASO :ANGULO
FIN
Este procedimiento genera una maravillosa colección de dibujos cuando lo usamos con entradas diferentes.
Aun cuando se indica que POLI tiene entradas, es en realidad un procedimiento de entradas fijas, porque una vez establecidos los valores de PASO y ANGULO estos no cambian. Para crear un procedimiento que no lo sea, cambiamos la última línea de POLI. Le cambiamos su título también, aun cuando no sea necesario hacerlo. El efecto de POLIESPI se muestra a continuación (POLIESPI 5 90 o CUADRIRAL)
PARA POLIESPI :PASO :ANGULO | |
Podemos ver que podemos usar POLI para dibujar un círculo. Podemos usarlo ahora para dibujar nuestro signo de la paz? Podríamos, pero nos irá mejor haciendo un procedimiento, aquí llamado ARCO cuyo efecto será el de dibujar cualquier segmento circular, dados el diámetro y el ángulo a dibujar. El procedimiento es como sigue. El asterisco "*" es usado para expresar multiplicación.
PARA ARCO :DIAM :SECTOR
SI :SECTOR = 0 [ALTO]
AVANZA :DIAM * 3.14159 / 180 / 2
GIRAIZQUIERDA 1
ARCO :DIAM :SECTOR - 1
FIN
Ahora podremos hacer un nuevo procedimiento utilizando nuestro antiguo procedimiento PAZ como un subprocedimiento .
PARA SUPERPAZ
GIRADERECHA 90
ARCO 200 360
GIRAIZQUIERDA 90
PAZ
FIN
Mejor aún, podríamos rescribir PAZ para que tenga entradas. Por ejemplo:
PARA PAZ :TAM
AVANZA :TAM
GIRADERECHA 60
AVANZA :TAM
RETROCEDE :TAM
GIRAIZQUIERDA 120
AVANZA :TAM
GIRAIZQUIERDA 90
ARCO 2 * :TAM 360
FIN
Signos de paz de tamaños diferentes pueden hacerse con los comandos:
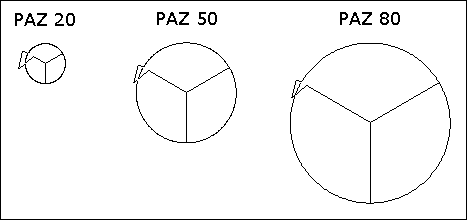
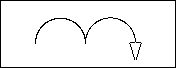
Podemos usar el comando ARCO para dibujar un corazón:
PARA CORAZON :TAM | |
*MiniTeorema:* Un corazón puede ser hecho a partir de cuatro arcos circulares.
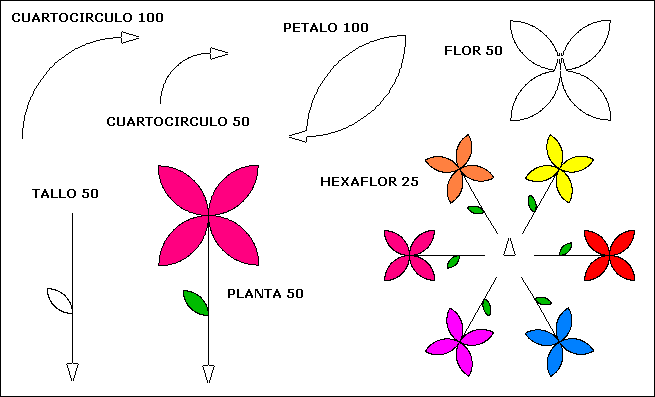
También podemos usar *ARCO* para dibujar una flor. Note en lo siguiente la construcción característica de nuevas definiciones a partir de viejas.
Un programa de computador, para dibujar esta flor, hace uso de la observación geométrica que los pétalos pueden ser descompuestos (para nuestra sorpresa!) en dos cuartos de círculo. Asumamos que tenemos un procedimiento llamado *CUARTOCIRCULO* cuyo efecto se muestra en los ejemplos.
PARA PETALO :TAM | PARA FLOR :TAM | PARA TALLO :TAM |
PARA PLANTA :TAM | PARA HEXAFLOR :TAM |
3. Cuáles son los Conceptos Primarios de las Matemáticas
El ver a los puntos y a las rectas como los conceptos primarios de la geometría es olvidar, no solamente las primitivas lógicas (como los cuantificadores) sino especialmente, las primitivas epistemológicas , tales como la noción de un sistema matemático en sí mismo. Para la mayoría de los niños en las escuelas, el problema no es que no comprenden estructuras o conceptos matemáticos particulares . Más bien, ellos no comprenden qué tipo de cosa es una estructura matemática: ellos no le encuentran sentido a emprender tal actividad. El pedirles que la aprendan es como pedirles que aprendan poesía en un lenguaje extranjero completamente desconocido.
A veces se dice que al enseñar matemáticas debemos enfatizar el proceso de matematización. Yo digo: excelente! Pero a condición de que el niño debe tener él mismo la experiencia de matematizar. De otra forma, la palabra "matematizar" es solamente otro término escolástico. El impulso de las exploraciones que he descrito es el permitir al niño tener experiencias vivas de matematización como introducción a las matemáticas.
...
Pero ¿cuáles son los ingredientes del proceso de matematización? ¿Es posible formular y enseñar conocimiento acerca de cómo uno debe abordar por ejemplo, el problema de establecer una representación matemática de un objeto tal como los corazones o flores que discutimos anteriormente?
Nuestra respuesta es una muy definitiva afirmación , especialmente en el contexto del trabajo descrito más arriba. Considere por ejemplo, cómo enseñaríamos a los niños cómo enfrentar problemas como dibujar un corazón. Como primer paso diríamos: si no puedes resolver el problema como se plantea, intenta simplificarlo; si no puedes encontrar una solución completa, encuentra una solución parcial. Sin duda todos dan consejos similares. La diferencia es que en este contexto el consejo es suficientemente concreto para ser seguido por un niño que parece insensible a las matemáticas usuales.
Una simplificación del problema del corazón es conformarse, como una primera aproximación, con un triángulo; el cual luego consideramos como un corazón muy primitivo.
PARA TRI | |
Ahora que tenemos esta construcción a mano podemos permitirnos modificarla para hacerla un mejor corazón. El plan obvio es reemplazar la línea horizontal por una línea estructural. Así que escribimos un procedimiento para hacer esto. Primero escojamos un nombre, digamos "PSUPERIOR", luego escribimos:
PARA PSUPERIOR :TAM | |
Reemplazando la primera línea del procedimiento TRI con PSUPERIOR obtenemos:
PARA TRI | |
El efecto es como se muestra! ¿Es un fracaso? Nosotros podríamos clasificarlo así (y a nosotros mismos!) si no tuviésemos otro concepto heurístico: DEFECTOS (BUGS) y DEPURACIÓN (DEBUGGING). Nuestro procedimiento no falló. Tiene un perfectamente comprensible ~defecto~ . Para encontrar el defecto revisamos el procedimiento de una manera muy ~formal~ (La formalidad es otro concepto que intentamos enseñar). Rápidamente descubrimos que el problema está en la segunda línea. También podemos ver porqué. El reemplazar la primera línea con FSUPERIOR hizo lo que deseábamos, pero también produjo un ~efecto secundario~ (otro concepto importante). Dejó a la tortuga apuntando en una dirección diferente. El corregirlo es simplemente cosa de cambiar la segunda línea a *GIRADERECHA 30* . Y luego podremos proseguir a hacer el corazón completamente curvado. A menos que decidamos que el de lados rectos es suficientemente bueno para nuestros propósitos.

Nuestra imagen de enseñar matemáticas se concentra en enseñar conceptos y terminología que permita al niño desenvolverse y expresarse acerca del proceso de desarrollar un análisis matemático. Una parte para lograr esto es estudiar buenos modelos (tal como la anécdota del corazón) y ganar experiencia describiendo los intentos propios para seguir el patrón del modelo en otros problemas. Parece bastante paradójico que al desarrollar planes de estudios de matemáticas, se consagran conferencias completas de matemáticos excelentes a discutir el lenguaje apropiado para expresar la parte ~formal~ de las matemáticas, mientras al maestro o escritor de libros de texto individual se le deja cómo (y aún, si es que ~conviene~ ) manejar conceptos heurísticos.
En resumen, hemos puesto de manifiesto tres tesis centrales:
- Las primitivas matemáticas no formales son descuidadas en las discusiones de los planes de estudios de matemáticas.
- Que la elección de contenido, especialmente para los primeros años, debería ser hecha principalmente en función de sus idoneidad para desarrollar conceptos heurísticos, y
- Las matemáticas computacionales, en el sentido ilustrado por la geometría de tortuga, tiene ventajas poderosas a este respecto, sobre los tópicos "clásicos".
4. Preguntas, Dudas, Comentarios, Peticiones
5. Enlaces
Logo como herramienta para mejorar la comprensión de las Matemáticas
Matemafobia: el Miedo de Aprender
Más escritos de Seymour Papert