El Problema de los Cumpleaños
Contenido
1. Tratamiento con simulaciones
Un grupo de personas está reunido en una habitación, ¿qué tan probable es que dos de ellas cumplan años el mismo día?
Para dar respuesta a esta cuestión podemos hacer una simulación con LogoFE. Imaginemos 5 personas en una habitación. Cada una de ellas habrá nacido en alguna fecha de las 365 que tiene un año (no bisiesto):
muestra clona [5 365]
[365 365 365 365 365]
muestra impon "azar clona [5 365]
[164 362 351 114 254]
Podemos ordenar estos números y agruparlos si hay varios que se repiten.
muestra ordena impon "azar clona [5 365]
[132 220 240 281 307]
muestra disgrega duplica ordena impon "azar clona [5 365]
[[27] [86] [189] [237] [354]]
Con un grupo de 5 es difícil encontrar dos que se repitan, pero con 30 ya es más fácil. En la siguiente simulación encontramos dos pares que representan a dos parejas de personas que tienen la misma fecha de nacimiento en el grupo:
muestra disgrega duplica ordena impon "azar clona [30 365]
[[3] [19] [38] [47] [62 62] [68] [79] [92] [97] [109] [117] [119] [122] [149] [150]
[159] [177] [202 202] [234 234] [236] [243] [324] [326] [332] [333] [345] [354]]
Si además, contamos cuantos miembros hay en cada grupo es fácil ver que en un grupo de 30 personas, sí suele ocurrir que dos de ellas cumplen años el mismo día, aunque no siempre:
muestra impon "cuenta disgrega duplica ordena impon "azar clona [30 365]
[1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
muestra impon "cuenta disgrega duplica ordena impon "azar clona [30 365]
[1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
muestra impon "cuenta disgrega duplica ordena impon "azar clona [30 365]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
muestra impon "cuenta disgrega duplica ordena impon "azar clona [30 365]
[1 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
Se nos ocurre que sería bueno poder hacer una simulación con un número determinado de personas y saber si se cumple o no que existe al menos una pareja de personas con la misma fecha de cumpleaños:
funciona "grupos [disgrega duplica ordena impon "azar clona dista 365]
muestra grupos 5
[[4] [70] [89] [100] [170]]
muestra grupos 5
[[35] [230] [281] [306] [342]]
muestra grupos 10
[[2] [15] [16] [85] [120] [148] [170] [280] [292] [333]]
muestra impon [dec cuenta] grupos 30
[0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
muestra impon [dec cuenta] grupos 30
[0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
muestra impon [dec cuenta] grupos 30
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
muestra suma impon [dec cuenta] grupos 30
2
muestra suma impon [dec cuenta] grupos 30
1
muestra suma impon [dec cuenta] grupos 30
0
muestra signo suma impon [dec cuenta] grupos 30
1
muestra signo suma impon [dec cuenta] grupos 30
0
muestra signo suma impon [dec cuenta] grupos 30
1
funciona "pareja? [signo suma impon [dec cuenta] grupos]
pareja? nos dirá si, en una simulación de un grupo de un cierto número de personas, hubo o no hubo al menos una pareja. 1 quiere decir cierto y 0 quiere decir falso.
muestra pareja? 30
1
muestra pareja? 30
1
muestra pareja? 30
0
Podemos hacer 20 simulaciones de grupos de 30, como si observáramos 20 habitaciones diferentes con 30 personas cada una:
muestra clona [20 30]
[30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30]
muestra impon "pareja? clona [20 30]
[0 1 1 1 1 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0]
muestra impon "pareja? clona [20 30]
[1 0 1 0 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 0]
Si promediamos lo que ocurre en todas estas habitaciones siempre obtendremos un valor entre 0 y 1, si en todas las habitaciones hay parejas el promedio será 1. Si en ninguna habitación hay pareja el promedio será 0. La probabilidad de un evento también se presenta como un valor entre 0 y 1. Así que nuestras simulaciones nos pueden dar una buena idea de cuál es la probabilidad teórica de que exista al menos una pareja de cumpleañeros para un grupo de cierto tamaño (mientras más habitaciones inspeccionemos para promediar, mejor):
funciona "prob.parejas.en.grupo [media impon "pareja? clona]
muestra serie [1 10 11]
[1 11 21 31 41 51 61 71 81 91 101]
haz "datos recorrido [prob.parejas.en.grupo lista 50 ?] serie [1 10 11]
escribemat :datos
1 11 21 31 41 51 61 71 81 91 101
0 0.12 0.46 0.78 0.94 1 1 1 1 1 1
En lo anterior usamos 50 habitaciones para cada grupo de personas. Investigamos varios grupos con diferente número de personas. En las habitaciones con sólo 1 persona nunca hubo dos personas con la misma fecha de cumpleaños. Esto no debería ser una sorpresa. Lo que quizá sí sea sorprendente es que en todas las 50 habitaciones con 51 personas hubo por lo menos una pareja. Por esta razón este problema también se conoce como la paradoja del cumpleaños.
LogoFE permite graficar los datos obtenidos así:
borrapantalla
graflineas [[Ptit: [Problema de los Cumpleaños]]
[Xtit: Personas]
[Ytit: Probabilidad]] :datos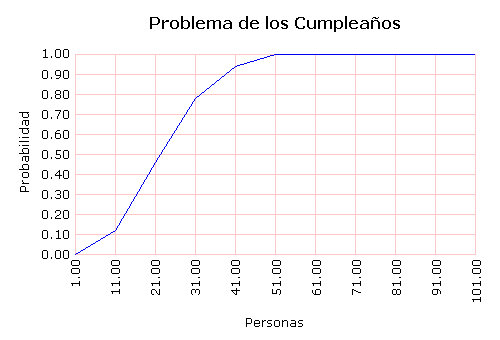
2. Preguntas, Dudas, Comentarios, Peticiones
3. Enlaces
Otra simulación para estimar el valor de PI

