Geometría Dinámica y Sistemas de Ecuaciones
Este es el problema:
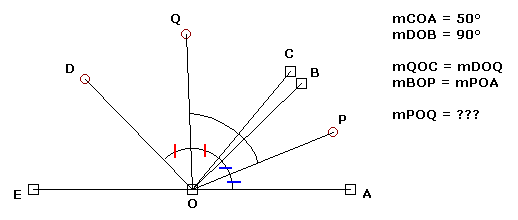
Mi primer impulso fue el de poner nombres más sencillos a los ángulos:
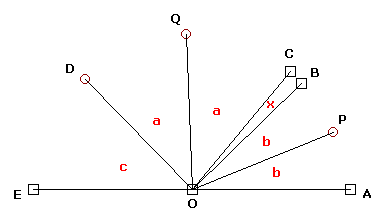
Luego pensé que sería buena idea expresar en ecuaciones la mayor cantidad de relaciones que encontrara en el diagrama para luego poder combinar varias de ellas para encontrar la solución. Esto lo hago porque generalmente estos problemas son cerrados, en el sentido de que generalmente presentan pocos o ningún dato superfluo (al contrario de lo que ocurre en problemas que se encuentran en la vida real). Planteé entonces estas ecuaciones.
- 2a + x = 90
- 2b + x = 50
- c + 2a + x + 2b = 180
- mPOQ = a + x + b
Pensé que para determinar la medida del ángulo POQ debería encontrar los valores de x, a y b y luego sumarlos. Pero esto resulta imposible ya que no tengo ningún conjunto de tres ecuaciones que involucren únicamente a x, a y b. Lo máximo que puedo hacer con las ecuaciones 1 y 2 es encontrar una relación entre a y b.
- 2a + x = 90
- 2b + x = 50
- x = 90 - 2a
- x = 50 - 2b
- 90 - 2a = 50 - 2b
- 40 = 2a - 2b
- 20 = a - b
Es decir, si tomo las dos primeras ecuaciones originales tengo un sistema de 2 ecuaciones con 3 incógnitas. Si tomo las ecuaciones originales: 1, 2 y 4 tengo un sistema de 3 ecuaciones y 4 incógnitas. Y si tomo todas la ecuaciones tengo un sistema con 4 ecuaciones y 5 incógnitas. Como sabía que los sistemas de ecuaciones lineales que tienen más incógnitas que ecuaciones tienen infinitas soluciones me parecía que me faltaba una ecuación adicional; algo que no había visto en el diagrama. Pasé algún tiempo tratando de encontrarla... sin exito.
La idea de que con los datos dados no existe un solución única podría reforzarse con una argumentación como la siguiente:
No existe relación entre el ángulo AOC y el ángulo BOD. Al no haber restricciones para el ángulo BOC, esta abertura puede variar y arrojar diferentes soluciones.
Este argumento fue compartido conmigo por un colega, Ezequiel Crespo de Venezuela, quien muy gentilmente quizó participar en el análisis de la resolución de este problema (en un breve intercambio de emails entre nosotros). Sin embargo, otra colega, Silvia Margeli de España, al ver la ecuación iii concluyó:
He pensado que lo que quedaba fijo era la relación entre dos ángulos, o sea que la estructura que propones se puede mover.
Luego ella me indicó que ella asoció inmediatamente la posibilidad de movimiento de esta construcción con una herramienta de geometría dinámica en la cual replicó la construcción de la siguiente manera:
... primero el ángulo de 50 y fijo, luego un segmento y una perpendicular para tener el de 90, y luego las bisectrices... La estructura se puede mover y el ángulo que pides mide siempre 70.
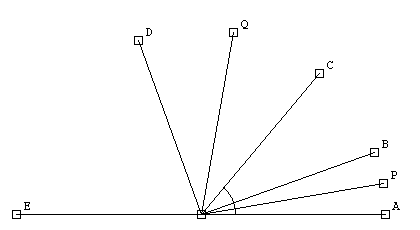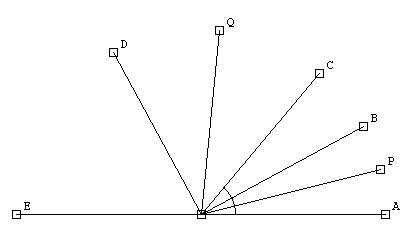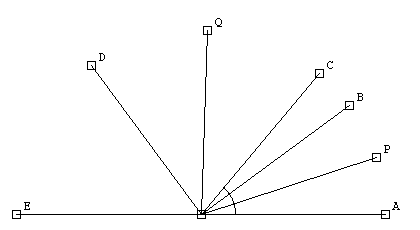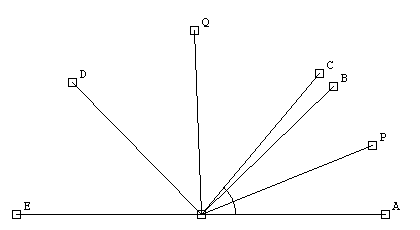
... y miro el dibujo. Cuando lo imaginas en movimiento da mucho de si. Si haces COB = 0 (nadie dice que no pueda serlo) entonces a vale 45 y b vale 25... Bonito, Si. :-)
Al poco tiempo de mostrarle este diagrama, Ezequiel me respondía:
Es cierto, ahora el problema para mi sería explicar por qué es fijo.
Por si le interesa el proceso que seguí para la solución, es este:
DOB + COA - COB = DOA
90 + 50 - COB = DOA
140 - COB = DOA
140 - COB = 2 COQ + 2 POB + COB
140 = 2 (POB + COB + COQ)
por lo tanto: POQ = 70.
El problema me dejo pensando sobre el hecho de que llegar a una respuesta en un problema no significa que esté resuelto; pueden existir otras formas de hacerlo o incluso, que no se haya tomado relaciones en cuenta y que como en este caso la respuesta sea otra.
Comparto plenamente con Ezequiel la idea de que llegar a una respuesta en un problema no significa que esté resuelto. Casi simultáneamente Víctor Mena, de Costa Rica, me envió el siguiente desarrollo algebráico que utiliza la notación de la figura 2, arriba:
Se tiene x + 2 a = 90 y x + 2 b = 50.
Sumando se obtiene 2 x + 2 a + 2 b = 140, de donde x + a + b = 70, es decir POQ mide 70º.
En el mismo mensaje decía:
Quiero exponer mi experiencia al dibujar la figura en mi PC, utilizando software de geometría en movimiento. Creo que el uso de esta tecnología es excelente para la exploración de problemas de este tipo, y es más fácil para el estudiante hacer conjeturas. El estudiante puede darle libre movimiento al DOB sin que las condiciones del problema se vean afectadas. Puede mover B y notar que la medida del QOP se conserva aún cuando B no está en el interior del COA. Se observa entonces que la medida del COB es irrelevante, pues gráficamente QOP siempre medirá lo mismo. Luego, para resolver el problema, hay al menos dos formas:
- Mover B hasta que pertenezca al rayo OC. Así, el DOA mide 90º + 50º = 140º, y como queda compuesto por dos parejas de ángulos iguales, se toma un ángulo de cada pareja y se tiene que el QOP debe medir la mitad de 140º.
- Mover B hasta que pertenezca al rayo OA. Puesto que COA mide 50º, el DOC debe medir 90º - 50º = 40º, y luego, el QOC debe medir 20º. Entonces QOA mide 50º + 20º = 70º.
- DOQ + QOC + COB = 90
- QOC + COB + BOP = X
- COB + BOP + POA = 50
- BOP = POA
- DOQ = QOC
Este sistema tiene 5 ecuaciones y 6 incógnitas y puede expresarse en forma matricial así:
| X | DOQ | QOC | COB | BOP | POA | N | |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 90 |
| 2 | -1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 50 |
| 4 | 0 | 0 | 0 | 0 | 1 | -1 | 0 |
| 5 | 0 | 1 | -1 | 0 | 0 | 0 | 0 |
Al aplicar el método de reducción matricial utilizando una herramienta de cálculo numérico...
haz "matriz [[0 1 1 1 0 0 90] [-1 0 1 1 1 0 0] [0 0 0 1 1 1 50] [0 0 0 0 1 -1 0] [0 1 -1 0 0 0 0]]
tabla!htm "fig ponprimero [[1 2 3 4 5] [X DOQ QOC COB BOP POA N]] redmat :matriz
... la matríz queda así:
| X | DOQ | QOC | COB | BOP | POA | N | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 70 |
| 2 | 0 | 1 | 0 | 0 | 0 | -1 | 20 |
| 3 | 0 | 0 | 1 | 0 | 0 | -1 | 20 |
| 4 | 0 | 0 | 0 | 1 | 0 | 2 | 50 |
| 5 | 0 | 0 | 0 | 0 | 1 | -1 | 0 |
La primera ecuación nos da la solución del problema: X = 70.
El conocer que con el método de reducción matricial puedo obtener soluciones numéricas de los sistemas de ecuaciones lineales que puedan darlas, o al menos relaciones más sencillas entre las incógnitas de aquellos sistemas que no pueden, ha añadido una herramienta poderosa a mi caja de herramientas personal para resolver problemas.
1. Licencia
Este es un documento libre.
Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
2. Preguntas, Dudas, Comentarios, Peticiones
3. Enlaces
Un Problema de Triángulos Interesante

