Problema de Triángulos
Este es uno de tantos problemas de triángulos ¿Cuánto miden los segmentos a y b?
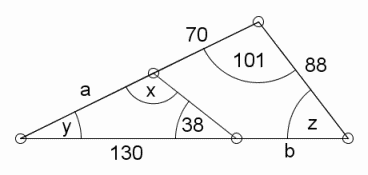
Añadimos unas letras para nombrar a los extremos de los segmentos que conforman la construcción.
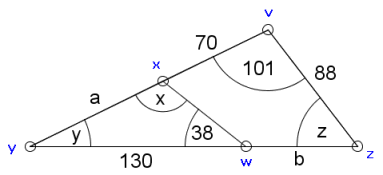
La primera cosa que notamos es que el triángulo yxw no es semejante al triángulo yvz, ya que los segmentos xw y vz no son paralelos. Consecuentemente el ángulo x no mide 101°, ni el ángulo z mide 38°. Que pena.
Nuestra estrategia será recorrer con la tortuga de Logo la trayectoria ywxvz. Cuando tengamos estos segmentos bien construidos pensamos hacer las mediciones necesarias para saber las longitudes de los segmentos a y b.
Empezamos orientando la tortuga hacia la derecha, avanzando los 130 pasos y girando los grados necesarios para formar el ángulo ywx
ponrumbo 90 avanza 130 giraizquierda 180 - 38
Nuestro primer obstáculo viene a continuación ya que no conocemos la longitud de wx; es una incógnita. Eso nos sugiere construir un procedimiento que reciba una entrada para que luego podamos jugar con esta incógnita.
para triangulo :wx
ponrumbo 90 avanza 130
giraizquierda 180 - 38 avanza :wx
fin
Luego con encontramos con el siguiente inconveniente: el ángulo wxv tampoco tiene un valor dado. Tendremos que definir otra entrada para nuestro procedimiento.
para triangulo :wx :wxv
ponrumbo 90 avanza 130
giraizquierda 180 - 38 avanza :wx
giraderecha 180 - :wxv
fin
Lo siguiente ya es más fácil. Avanzamos 70 pasos, giramos lo necesario para formar el ángulo de 101° y avanzamos 88 pasos.
para triangulo :wx :wxv
ponrumbo 90 avanza 130
giraizquierda 180 - 38 avanza :wx
giraderecha 180 - :wxv avanza 70
giraderecha 180 - 101 avanza 88
fin
Con nuestro procedimiento listo podemos empezar a jugar. Adivinamos la longitud de wx; probablemente sea menor que 88 ya que vz tiene una longitud de 88 y parece más largo. También adivinamos un tamaño para el ángulo wxv; parece un poco más grande que ywx que sabemos tiene 38°. Intentamos con 40 y 80 primero y luego con 40 y 50. (Al parecer los científicos prefieren jugar con una variable a la vez).
borrapantalla triangulo 60 80
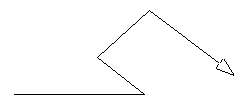
borrapantalla triangulo 60 50

Vemos que estas construcciones están mal, pero gracias a que las hicimos podemos darnos cuenta de varias cosas. Para que la construcción esté bien la posición final de la tortuga debe estar alineada al segmento yw (el horizontal). Además, el segmento xv no se ve bien. En la primera construcción está muy parado (vertical) y en la segunda está demasiado acostado (horizontal). De extender el segmento xv este debería tocar el punto y (el punto de partida de la tortuga). Esto nos da la idea de que cuando la tortuga está en el punto x debería tomar el rumbo opuesto al que tomaría si deseara llegar al punto y. Por lo que modificamos el procedimiento.
para triangulo :wx
ponrumbo 90 avanza 130
giraizquierda 180 - 38 avanza :wx
ponrumbo (180 + hacia [0 0]) avanza 70
giraderecha 180 - 101 avanza 88
fin
Al realizar esta modificación vemos que el procedimiento ya no necesita de wxv como entrada. Ahora juguemos con la longitud del segmento wx.
borrapantalla triangulo 80
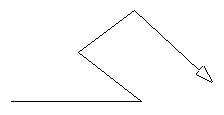
borrapantalla triangulo 50
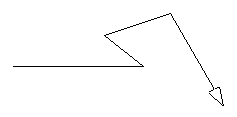
Vemos que, si damos al segmento wx una longitud de 80, la posición final de la tortuga no logra alinearse con el segmento horizontal. Está por encima. Pero cuando le damos una longitud de 50 tampoco logra alinearse porque está por debajo. Si recordamos algo del plano cartesiano sabremos que el segmento horizontal (yw) esta justamente en el eje X, es decir todos sus puntos tienen, en su coordenada Y, el valor de 0. Lo mismo debería ocurrir con la posición final de la tortuga: el punto z debe tener una coordenada Y igual a 0. ¿Cuál es la coordenada Y de z en las construcciones anteriores? Logo nos lo puede decir.
para triangulo :wx
borrapantalla
ponrumbo 90 avanza 130
giraizquierda 180 - 38 avanza :wx
ponrumbo (180 + hacia [0 0]) avanza 70
giraderecha 180 - 101 avanza 88
devuelve ycor
fin
escribe triangulo 80
31.093912
escribe triangulo 50
-23.086427
Ahora el procedimiento triangulo se ha convertido en una función que recibe un número y devuelve otro. Deseamos encontrar un valor para entregar a triangulo que resulte en O.
Existen varios métodos numéricos para hacer justamente esto. Uno consiste en ir acorralando al valor de buscamos: ya que sabemos que 80 es muy alto y 50 es muy bajo el valor que buscamos debe estar entre los dos. Quizá sea el valor que está a medio camino entre 80 y 50, es decir 75... Este método se llama método de bisección y puede ser programado en Logo.
Otro método podría ser intentar muchos valores entre 50 y 80, y finalmente quedarnos con el que al pasárselo a triangulo produzca un número muy cercano a 0. Aún otro método podría ser realizar una gráfica comparando valores de entrada a triangulo con valores de salida de triangulo:
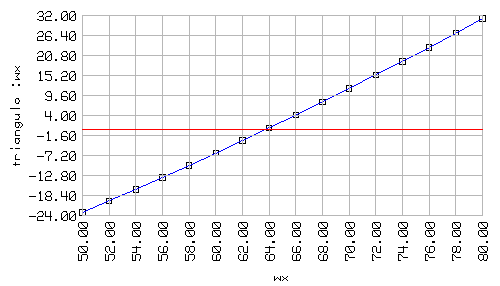
Esta gráfica fue preparada con LogoFE y de por ella sabemos que la longitud de wx es muy cercana a 64, pero:
escribe triangulo 64
0.506754
LogoFE también implementa un método numérico para encontrar los valores que hacen 0 a una función.
escribe resuelve "triangulo [50 80]
63.7172554751669
escribe triangulo 63.7172554751669
0
¿Y cuánto miden los segmentos a y b? Bueno, midamos:
para triangulo :wx
borrapantalla
ponrumbo 90 avanza 130
haz "w pos
giraizquierda 180 - 38 avanza :wx
haz "a distancia [0 0]
ponrumbo (180 + hacia [0 0]) avanza 70
giraderecha 180 - 101 avanza 88
haz "b distancia :w
haz "z rumbo - 90
devuelve ycor
fin
escribe resuelve "triangulo [50 80]
63.7172554751669
escribe :a
88.9118612730876
escribe :b
65.789731
escribe :z
52.8192805810521
¿Será cierta tanta maravilla?
para triangulo.resuelto :a :b :z
ponrumbo 90 avanza 130 + :b
giraizquierda 180 - :z avanza 88
giraizquierda 180 - 101 avanza 70 + :a
fin
para triangulo :wx
ponrumbo 90 avanza 130
giraizquierda 180 - 38 avanza :wx
ponrumbo (180 + hacia [0 0]) avanza 70
giraderecha 180 - 101 avanza 88
fin
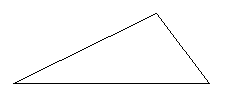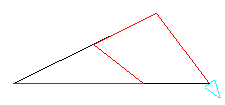
borrapantalla
poncolorlapiz 0 triangulo.resuelto 88.9118612730876 65.789731 52.8192805810521
poncolorlapiz 4 triangulo 63.7172554751669
1. Licencia
Este es un documento libre.
Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
2. Preguntas, Dudas, Comentarios, Peticiones
3. Enlaces
Más ejercicios sobre Construcción de Triángulos

