Puntos de Intersección de dos Círculos con LogoFE
Contenido
2. Solución Propuesta usando LogoFE
3. Procedimientos Auxiliares
4. Licencia
5. Preguntas, Dudas, Comentarios, Peticiones
6. Enlaces
1. Anterior Solución Propuesta
Existe ya una solución propuesta usando simplemente Logo, para encontrar los puntos de intersección de dos círculos. En aquella ocasión generamos puntos al azar, de uno y otro círculo hasta encontrar dos que estuviesen suficientemente cerca.
2. Solución Propuesta usando LogoFE
En esta oportunidad usaremos un procedimiento punto.de.circulo que devuelve un punto correspondiente a un círculo de posición y radio dados. El punto devuelto estará determinado por un ángulo también dado.
para punto.de.circulo :pos :radio :angulo
devuelve sumacomp lista :pos polrec lista :radio :angulo
fin
El procedimiento punto.de.circulo devuelve la suma de dos números complejos: el primero representa el vector del origen al centro del círculo, y el segundo de longitud igual al radio del círculo y en el ángulo dado. (La relación entre los números complejos y la geometría analítica plana debería ser más resaltada cuando se estudian estos números).
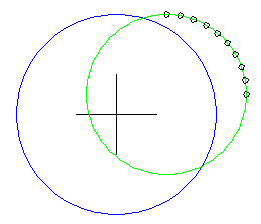
Para la exposición usaremos las mísmas circunferencias anteriores. La circunferencia azúl está centrada en el origen, mientras que la circunferencia verde está centrada en (50,20).
A continuación dibujamos varios puntos del círculo verde, correspondientes a los ángulos dados: 0, 10, 20, 30, 40, 50, 60, 70, 80, 90.
borrapantalla | |
Como vemos en el dibujo anterior, a medida que vamos aumentando el *ángulo* dado a *punto.de.circulo*, la distancia entre los puntos devueltos y la circunferencia azúl, se hace más pequeña. Sabemos que todos los puntos de la circunferencia azúl deben estar a 100 unidades del centro de ella (ya que la circunferencia azúl tiene una radio de 100).
Sabremos que hemos encontrado un punto de intersección cuando la distancia entre un punto devuelto por *punto.de.circulo* y el centro de la circunferencia azúl sea 100, o cuando la diferencia entre esa distancia y 100 sea cero. Veamos cúando se hace cero esa diferencia:
borrapantalla graflineas [[SuIn: [100 -100]]] ~
recorrido [(distan [0 0] punto.de.circulo [50 20] 80 ?) - 100] ~
dominio [0 360 100]
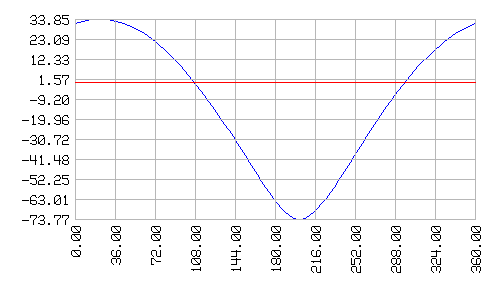
Vemos que una solución está cerca de 108 y que la otra está cerca de 300. En todo caso, la primera solución está entre 0 y 180, mientras que la otra está entre 180 y 360. A continuación mejores aproximaciones:
haz "ang1 resuelve [100 - distan [0 0] punto.de.circulo [50 20] 80] [0 180]
haz "ang2 resuelve [100 - distan [0 0] punto.de.circulo [50 20] 80] [180 360]
escribe :ang1
107.141466633695
escribe :ang2
296.461352339009
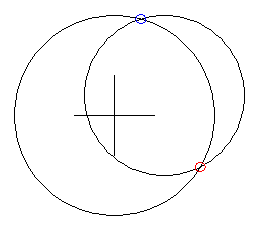
Entonces los puntos serán:
escribe punto.de.circulo [50 20] 80 :ang1 | |
borrapantalla
poncolorlapiz 0 dibuja.centro
dibuja.circulo [0 0] 100
dibuja.circulo [50 20] 80
poncolorlapiz 1 dibuja.circulo punto.de.circulo [50 20] 80 :ang1 5
poncolorlapiz 4 dibuja.circulo punto.de.circulo [50 20] 80 :ang2 5
3. Procedimientos Auxiliares
para dibuja.centro
avanza 40 retrocede 80 avanza 40 giraizquierda 90
avanza 40 retrocede 80 avanza 40 giraderecha 90
fin
para dibuja.circulo :pos :radio
subelapiz ponpos :pos
bajalapiz circulo :radio
fin
para distan :p1 :p2
haz "dx (primero :p1) - (primero :p2)
haz "dy (ultimo :p1) - (ultimo :p2)
devuelve raizcuadrada :dx * :dx + :dy * :dy
fin
4. Licencia
Este es un documento libre.
Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.