Puntos de Intersección de dos Círculos
Contenido
2. Procedimientos Auxiliares
3. Licencia
4. Preguntas, Dudas, Comentarios, Peticiones
5. Enlaces
1. Solución Propuesta
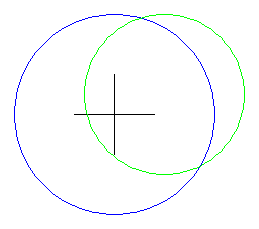
Trabajerémos con un par de circunferencias de ejemplo. La circunferencia azúl está centrada en el origen, mientras que la circunferencia verde está centrada en (50,20):
borrapantalla | |
Si se nos pidiera encontrar un punto cualquiera de la circunferencia azúl, podríamos proceder de la siguiente manera:
Ya que el radio de esa circunferencia es 100, y está centrada en el origen, escogeríamos una valor al azar entre -100 y 100 para la coordenada X:
borrapantalla
poncolorlapiz 0 dibuja.centro
poncolorlapiz 1 dibuja.circulo [0 0] 100
poncolorlapiz 0
repite 20 [dibuja.circulo (lista 2 * 100 - numero.entre.0.y.1 - 100 0) 3]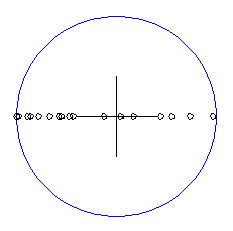
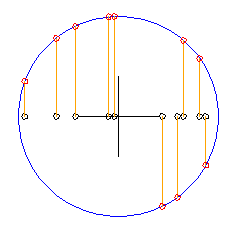
Luego calcularíamos el correspondiente valor para la coordenada Y, considerando que la distancia entre el punto (X,Y) y el origen debe ser igual al radio de la circunferencia. Es decir, usando el Teorema de Pitágoras:
radio · radio = x · x + y · y x · x + y · y = radio · radio y · y = radio · radio - x · x y = (+ o -) raizcuadrada (radio · radio - x · x) |
borrapantalla
poncolorlapiz 0 dibuja.centro
poncolorlapiz 1 dibuja.circulo [0 0] 100
haz "radio 100
repite 10 [
haz "x 2 * :radio * numero.entre.0.y.1 - :radio
haz "y mas.o.menos * raizcuadrada :radio * :radio - :x * :x
poncolorlapiz 0 dibuja.circulo (lista :x 0) 3
poncolorlapiz 14 subelapiz ponxy :x 0 bajalapiz ponxy :x :y
poncolorlapiz 4 dibuja.circulo (lista :x :y) 3
]
De esta manera podemos crear un procedimiento que devuelva un punto al azar de una circunferencia de radio dado, centrada en el origen:
para punto.de.circulo :radio
haz "x 2 * :radio * numero.entre.0.y.1 - :radio
haz "y mas.o.menos * raizcuadrada :radio * :radio - :x * :x
devuelve lista :x :y
fin
borrapantalla
dibuja.centro
repite 100 [dibuja.circulo (punto.de.circulo 100) 2]
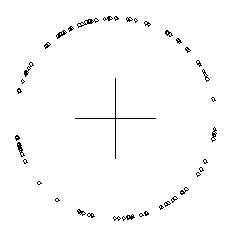
El procedimiento debe ser modificado para permitir que el centro de la circunferencia esté en cualquier coordenada:
para punto.de.circulo :pos :radio
haz "dx primero :pos
haz "dy ultimo :pos
haz "x 2 * :radio * numero.entre.0.y.1 - :radio
haz "y mas.o.menos * raizcuadrada :radio * :radio - :x * :x
haz "x :x + :dx
haz "y :y + :dy
devuelve lista :x :y
fin
borrapantalla
poncolorlapiz 0 dibuja.centro
poncolorlapiz 1 repite 100 [dibuja.circulo (punto.de.circulo [0 0] 100) 2]
poncolorlapiz 2 repite 100 [dibuja.circulo (punto.de.circulo [50 20] 80) 2]
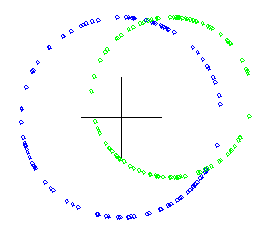
Tomemos un punto del círculo azúl y uno del círculo verde:
haz "pc1 punto.de.circulo [0 0] 100
haz "pc2 punto.de.circulo [50 20] 80
escribe :pc1
-86.5877616 -50.0255888631165
escribe :pc2
58.49691424 -59.5474854938739
Ya que estos puntos no coinciden, no pueden ser los que buscamos. Podríamos conformarnos con dos puntos que estén muy, muy cerca. Veamos qué distancia hay entre pc1 y pc2:
para dist :p1 :p2
haz "dx (primero :p1) - (primero :p2)
haz "dy (ultimo :p1) - (ultimo :p2)
devuelve raizcuadrada :dx * :dx + :dy * :dy
fin
escribe dist :pc1 :pc2
145.396800786829
La estrategia que usaremos es tomar dos puntos cualesquiera, uno del círculo azúl y otro del círculo verde, y calcular su distancia. Nos detendremos cuando por suerte encontremos dos que estén muy, muy cerca:
para encuentra.interseccion :error
haz.hasta [
haz "pc1 punto.de.circulo [0 0] 100
haz "pc2 punto.de.circulo [50 20] 80
haz "dist dist :pc1 :pc2
] [:error > :dist]
devuelve :dist
fin
escribe encuentra.interseccion 0.2
0.0468029686130622
Este resultado apareció a los pocos minutos. Indica la distancia entre los dos puntos encontrados, que es menor que el máximo error pedido. Las coordenadas de los puntos son:
escribe :pc1
26.4382896 96.4417795513258
escribe :pc2
26.47935392 96.4642348289668
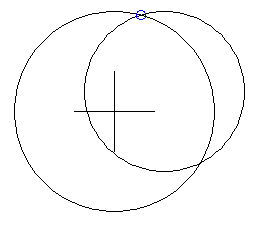
Vemos que en realidad pc1 y pc2 están visualmente uno sobre el otro. Y que coinciden con una de las intersecciones de los círculos:
borrapantalla | |
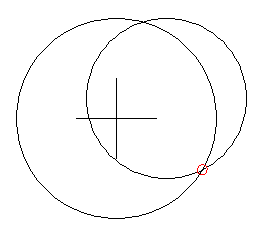
Luego de otros intentos, encontramos una aproximación para el otro punto:
escribe encuentra.interseccion 0.2borrapantalla | |
2. Procedimientos Auxiliares
para dibuja.centro
avanza 40 retrocede 80 avanza 40 giraizquierda 90
avanza 40 retrocede 80 avanza 40 giraderecha 90
fin
para dibuja.circulo :pos :radio
subelapiz ponpos :pos
bajalapiz circulo :radio
fin
para numero.entre.0.y.1
devuelve (azar 1000000000) / 1000000000
fin
para mas.o.menos
devuelve (2 * azar 2) - 1
fin
3. Licencia
Este es un documento libre.
Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
4. Preguntas, Dudas, Comentarios, Peticiones
5. Enlaces
Puntos de Intersección de dos Círculos con LogoFE