Raíz cuadrada de un número por el método de Newton
Contenido
1. Solución Propuesta
El método dice que, dada una ecuación f(x)=0, el valor de x puede irse aproximando mediante esta relación de recurrencia:
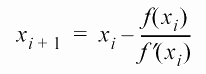
¿Cuál debe ser nuestra función?
Queremos encontrar el valor x de la siguiente ecuación:
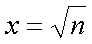
para un valor conocido de n.
Entonces:
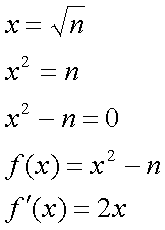
es decir:
para f :x
devuelve :x * :x - :n
fin
para f' :x
devuelve 2 * :x
fin
El procedimiento aproxima da un valor inicial a x de 1 y luego usa la relación de recurrencia 10 veces mostrando cada vez la aproximación obtenida:
para aproxima :n
escribe frase [Aproximando la Raíz Cuadrada de:] :n
haz "x 1
repite 10 [haz "x :x - (f :x) / (f' :x) escribe.aproximación]
fin
El procedimiento escribe.aproximación imprime tres números en una línea mostrando: la aproximación, el valor de la raíz cuadrada calculada internamente, y la diferencia entre ambos.
para escribe.aproximación
escribe `[
,[formatonumero (:x) 20 16]
,[formatonumero (raizcuadrada :n) 20 16]
,[formatonumero (abs :x - raizcuadrada :n) 20 16]
]
fin
aproxima 2
Aproximando la Raíz Cuadrada de: 2
1.5000000000000000 1.4142135623730951 0.0857864376269049
1.4166666666666667 1.4142135623730951 0.0024531042935716
1.4142156862745099 1.4142135623730951 0.0000021239014147
1.4142135623746899 1.4142135623730951 0.0000000000015947
1.4142135623730951 1.4142135623730951 0.0000000000000000
1.4142135623730949 1.4142135623730951 0.0000000000000002
1.4142135623730951 1.4142135623730951 0.0000000000000000
1.4142135623730949 1.4142135623730951 0.0000000000000002
1.4142135623730951 1.4142135623730951 0.0000000000000000
1.4142135623730949 1.4142135623730951 0.0000000000000002
aproxima 961
Aproximando la Raíz Cuadrada de: 961
481.0000000000000000 31.0000000000000000 450.0000000000000000
241.4989604989604900 31.0000000000000000 210.4989604989604900
122.7391368467891500 31.0000000000000000 91.7391368467891510
65.2843751618499080 31.0000000000000000 34.2843751618499080
40.0022947858842950 31.0000000000000000 9.0022947858842954
32.0129582795904640 31.0000000000000000 1.0129582795904639
31.0160260802395910 31.0000000000000000 0.0160260802395911
31.0000041403635510 31.0000000000000000 0.0000041403635507
31.0000000000002770 31.0000000000000000 0.0000000000002771
31.0000000000000000 31.0000000000000000 0.0000000000000000
2. Licencia
Este es un documento libre.
Autor: Daniel Ajoy

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
3. Preguntas, Dudas, Comentarios, Peticiones
4. Enlaces
Generado con PureJoy. Creación: 11:49 - Dec 15, 2017. Última Modificación: 17:12 - Apr 02, 2023

