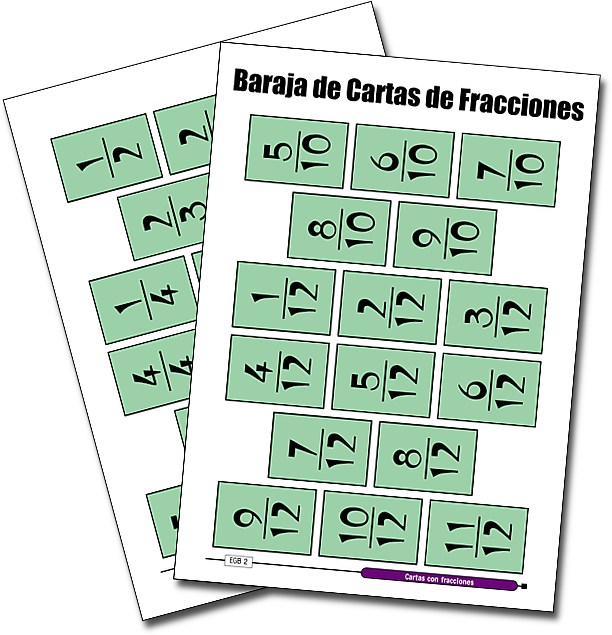
Baraja de Cartas de Fracciones

Utiliza la clave neoparaiso.com para abrir el PDF.

Contenido

1. Guerra de fracciones

Nº de jugadores: Se juega en grupos de 4 alumnos.

Material: 48 naipes con fracciones representadas en forma numérica en una cara y en forma gráfica en la otra.

1.1. Reglas del juego

Se mezclan y se reparten 12 cartas a cada jugador con la representación numérica hacia arriba, formando 4 pilas personales. Los 4 colocan a la vez en el centro, la carta superior de su pila.

Es un juego de comparar fracciones. El que tiene la carta de mayor valor se lleva las cuatro cartas y las coloca aparte en otra pila personal. Las cartas llevadas no se vuelven a usar.

Si hay dudas, se pueden dar vuelta las cartas y usar la comparación de los rectángulos pintados al dorso para constatar. Si hay empate se juega otra vuelta y el ganador se lleva las ocho cartas.

Gana quien al final del juego tiene más cartas.

1.2. Observaciones

Según el repertorio de fracciones que los alumnos estén manejando, se puede jugar con diferentes mazos, armados con algunas cartas seleccionadas entre las 48 del mazo. En tal caso, a cada jugador le tocarán menos cartas. Por ejemplo, con denominadores 2, 4 y 8, ó con 2, 3 y 6, ó con 2, 3, 4, 6 y 12.

Es un juego de comparación de fracciones a partir de su representación numérica y, en una segunda instancia, de una representación geométrica, en este caso un rectángulo. Esta comparación permitirá reconocer fracciones equivalentes como expresiones de la misma cantidad.

También puede ser interesante, en un momento de reflexión, proponer la comparación de ambas representaciones con otras trabajadas anteriormente.

Se puede agregar la regla de que el que se lleva cartas debe anotar todas las cartas de la mano señalando la ganadora para tener un registro escrito utilizable para la puesta en común.

Es conveniente que el docente genere un espacio para recuperar las distintas estrategias de comparación desarrolladas por los alumnos durante el juego. Convendrá detenerse tanto en el orden en que se van comparando como en los elementos tenidos en cuenta para establecer la comparación: los numeradores, los denominadores, su diferencia, la parte del entero que representa cada fracción, lo que le falta a cada una para completar la unidad, u otras que puedan surgir.

1.3. Posibles variantes

1.3.1. Guerra con cálculos

Se puede introducir la regla de que cada alumno dé vuelta dos cartas a la vez y las sume; y que se lleve todas el que obtenga la suma mayor. También, en forma análoga, se puede pedir que las reste y se lleve las cartas el que tenga la resta cuyo resultado sea el mayor o el menor.

Esto permitirá que los alumnos utilicen diferentes estrategias para sumar o restar fracciones y también para comparar los resultados. Podrán hacerlo comparando las representaciones geométrica o numérica de las fracciones que resultan en cada caso, o comparando las cartas una a una.

En caso de realizar la operación podrán utilizar o no equivalencias para obtener los resultados.

También en estos casos es conveniente solicitarles que registren por escrito los resultados obtenidos en algunas de las rondas, para facilitar una posterior puesta en común.

1.3.2. Poner orden

Modificar el juego inicial: cuando los cuatro jugadores dieron vuelta su carta, ordenarlas de mayor a menor, asignando puntos de 4 a 1, según ese orden. Gana el que obtiene más puntos.

En este caso no es necesario desempatar ya que puede haber jugadores con el mismo puntaje en esa ronda, si tenían tarjetas con fracciones equivalentes. Además, las cartas ya jugadas, pasan a un pozo común.

Este cambio involucra un proceso de comparación más complejo, ya que se deben comparar todas las cartas entre sí para establecer el orden entre ellas.

1.4. Actividades complementarias

Se pueden proponer actividades que simulen rondas de los juegos en sus diversas variantes.

Se podrá pedir que, en situaciones de comparación, de suma o de resta, determinen tanto el ganador como las cartas componentes de una jugada.

Por ejemplo: a partir del dibujo de las cuatro cartas descubiertas en una partida donde se las lleva el que tiene la mayor, preguntar: "¿Hay un ganador o es necesario desempatar? Expliquen por qué".

O para la variante con suma o con resta, dibujar 4 pares de cartas y preguntar cuál es el ganador, o dado el ganador y las cartas de tres jugadores, pedir que escriban posibles pares de cartas correspondientes al cuarto jugador.

En cuanto a la variante de establecer un orden, se puede proponer completar una serie con distintas posibilidades dadas dos o tres de las cuatro cartas.

2. Escoba Fraccionada

Es una baraja compuesta por 48 cartas distribuidas de la siguiente forma:

• 9 cartas de la fracción 1/12.
• 6 cartas de cada una de las fracciones 1/6, 1/4 y 1/3.
• 3 cartas de cada una de las fracciones 5/12, 1/2, 7/12, 2/3, 3/4, 5/6 y 11/12.

En cada una de las cartas aparece escrita la fracción que representa y también representada como la parte correspondiente de un hexágono. Las cartas representan todas las posibles fracciones múltiplos de 1/12.

2.1. Reglas del juego

Una vez elegido el jugador que comienza, se desarrolla según las siguientes reglas:

1. Cada jugador recibe dos cartas y se dejan otras cuatro sobre la mesa colocadas boca arriba.
2. Por turno, cada jugador tiene que conseguir que entre una de sus cartas y una o varias de las que hay sobre la mesa sumen la unidad. Cuando eso ocurre, todas las cartas que suman la unidad las guarda el jugador que lo ha logrado (y ya no intervienen esas cartas en la partida)
3. Si en el momento en que le toca a un jugador no hay cartas sobre la mesa o no consigue sumar la unidad, echa una de sus cartas boca arriba sobre la mesa y pasa el turno al jugador siguiente.
4. Cuando todos los jugadores han utilizado sus dos cartas, se reparten otras dos cartas a cada uno de los jugadores, y se continúa el proceso hasta que se acaban las cartas. Si en el último reparto sobran cartas, se colocan boca arriba sobre la mesa.
5. Si uno de los jugadores echa una carta sobre la mesa y pudiendo sumar la unidad (y por tanto llevarse cartas) no lo hace, las cartas serán para el primer jugador que se de cuenta de la posibilidad.
6. Las cartas que queden sobre la mesa al finalizar el juego no se contabilizan para ningún jugador.
7. Finalizado el juego se otorga a cada jugador un punto por cada una de las cartas que tenga. Gana la partida el primer jugador que llega a una puntuación prefijada de antemano (una posibilidad es 75, pero puede variar en función del tiempo que se disponga o de la destreza de los jugadores).

2.2. Posibles variantes

Una vez que los jugadores están entrenados en el juego pueden hacerse diferentes variantes. Entre ellas, las siguientes:

• Aumentar el número de cartas que se reparten cada vez hasta 3 o incluso 4.
• Dar una puntuación extra a algunas cartas con las que resulta más difícil sumar 1. Por ejemplo, la carta 11/12 puede valer 2 ó 3 puntos.
• Dar una puntuación extra de 5 puntos al jugador que al sumar la unidad se lleve todas las cartas que haya en ese momento sobre la mesa: es una “escoba”.
• Contabilizar las cartas sobrantes al finalizar la partida para el último jugador que se haya llevado cartas.

2.3. Objetivos

• Potenciar la operatividad de la suma de fracciones.
• Visualizar la representación gráfica del mecanismo de la suma de fracciones. Como en cada carta aparece una fracción múltiplo de 1/12 de un hexágono regular, se puede observar la manera en que distintas partes forman la unidad.
• Potenciar el desarrollo del cálculo mental.
• Buscar estrategias beneficiosas para el jugador.

2.4. Observaciones

Este juego requiere un cierto dominio previo de la suma de fracciones, por lo que los inicios son un poco lentos. Ayudan a interiorizar la dinámica las figuras que acompañan a las fracciones: sumar la unidad consiste en lograr entre todas las cartas un hexágono completo.

Puesto que el objetivo del juego es conseguir el mayor número posible de cartas, habrá que ver que hay distintas posibilidades de lograrlo, y no todas tienen el mismo número de sumandos. Por eso es conveniente dedicar alguna sesión previa a la obtención de todas las posibilidades de sumar la unidad.

3. Formar Familias

Se necesita un juego de cartas para cada equipo de cuatro alumnos.

El profesor se queda con todas las cartas que muestran porcentajes en su mano y reparte el resto entre los alumnos de la clase. A continuación muestra una carta sobre la mesa e invita a los que tengan otra carta equivalente a colocarla junto a la suya.

Después de esta fase inicial, ya podemos dar comienzo al juego, cuyas reglas son las siguientes:

Se reparten las 48 cartas entre los componentes del grupo. Cada jugador cede por turno al jugador que tiene a su derecha una carta; la que él quiera. El juego consiste en formar familias de cuatro cartas equivalentes. Cada jugador se descarta de aquéllas familias que vaya formando. Gana la partida el primer jugador que se quede sin cartas.

4. Completando Enteros

Grupos de 4 alumnos.

Se necesita una baraja para cada equipo.

Se trata de completar enteros (1, 2, 3, …) usando las fracciones que contienen varias cartas. Se reparten todas las cartas. Cada jugador roba una carta al anterior e intenta completar un número entero. Si lo consigue, deja las cartas que use sobre la mesa.

Gana el primer jugador que se queda sin cartas.

5. Blackjack (21)

Nº de jugadores: 2 o más.

Este juego se llama en realidad Blackjack es 1, y es un juego que los estudiantes disfrutan. Se aplican las mismas reglas que en el Blackjack. En lugar de tratar de llegar a 21, tratan de acercarse a 1 sin pasarse. Con este juego ellos practican suma de fracciones y comparar de fracciones. También puede hacer que sea más difícil o incluir números mixtos con Blackjack "2" Blackjack "3". (Blackjack 2 significa tratar de llegar lo más cerca posible a 2 sin pasarse.)

6. Poto sucio

Según Wikipedia:

El poto sucio es un juego de naipes en el que el objetivo es descartarse de todas los naipes. En cada ronda un jugador distinto esconde una carta al azar bajo sus glúteos (se supone que se encuentra sentado) -de ahí el nombre- sin que nadie la vea (ni siquiera él mismo). Luego se reparten 12 cartas, de las cuales cada jugador debe formar parejas de números (por ejemplo: 2 de corazón y 2 de trébol) la pinta da lo mismo, sólo el número debe ser igual, eso sólo con las 12 cartas que tiene en su mano. Después, cada jugador debe sacar una carta del mazo (o pozo) por turno y con esas cartas se siguen formando las parejas. Una vez que se acaban las cartas del pozo, entre los jugadores deben quitarse una carta por turno (sin que las vea el oponente, o sea el que está sacando la carta) y así seguir formando parejas. El jugador que se queda sin poder hacer la última pareja (porque esa es la carta que se ha escondido) es el poto sucio.

6.1. Reglas del juego

• Antes de repartir las cartas se esconde una (sin que nadie sepa cuál es)
• Se reparten 10 cartas por jugador, dejando el resto en montón sobre la mesa.
• Los jugadores forman todas las parejas que les ha tocado y las ponen sobre la mesa, boca arriba para que todos puedan comprobar las parejas.
• El juego comienza con las cartas que le han quedado a cada jugador/a.
• Mientras quedan cartas en el montón en cima de la mesa, cada uno va cogiendo una carta por turno y forman si pueden una nueva pareja.
• Cuando no quedan cartas en el montón, cada jugador ofrece al siguiente sus cartas, sin que el/ella las vea, para elegir una. Se forma, si se puede, una nueva pareja.

Gana el primero que se quede sin cartas. Se sigue jugando hasta que cada uno termine sus cartas. El último que se quede con una carta desparejada será el POTO SUCIO.

7. Baraja de Fracciones

Las barajas de fracciones se utilizan como material de enseñanza en las escuelas por varias razones:

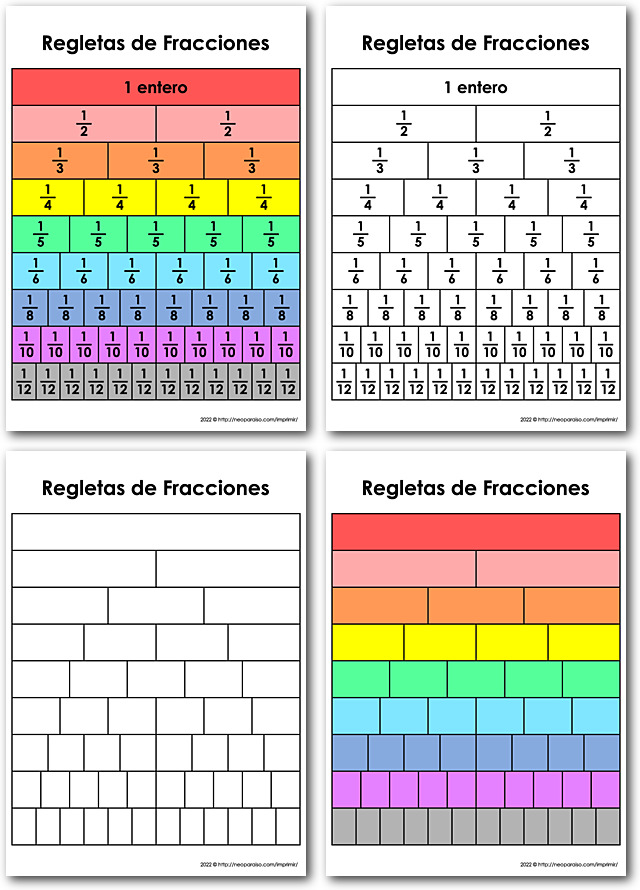
• Visualización: Las fracciones pueden ser un concepto abstracto para algunos estudiantes. Las barajas de fracciones proporcionan representaciones visuales de las fracciones, lo que ayuda a los estudiantes a comprender mejor conceptos como partes de un todo, comparaciones de tamaños y operaciones con fracciones.
• Manipulación: Al manipular las tarjetas de fracciones, los estudiantes pueden interactuar directamente con los conceptos matemáticos. Pueden mover las tarjetas, compararlas, agruparlas y dividirlas para explorar diferentes aspectos de las fracciones. Esta manipulación física puede ayudar a reforzar la comprensión de los conceptos.
• Adaptabilidad: Las barajas de fracciones son versátiles y pueden adaptarse para satisfacer las necesidades individuales de los estudiantes. Los maestros pueden usarlas en actividades grupales o individuales, en lecciones guiadas o en centros de aprendizaje independiente. Además, las tarjetas de fracciones se pueden utilizar en una variedad de contextos, desde juegos educativos hasta actividades de resolución de problemas.

Las barajas de fracciones son una herramienta efectiva para enseñar y reforzar conceptos relacionados con las fracciones en las escuelas debido a su capacidad para visualizar, manipular, practicar y adaptarse a las necesidades de los estudiantes.

LO MÁS DESCARGADO

Otros también vieron:

Fracciones

Juegos

Operaciones Mixtas

Tarjetas

Síguenos en Facebook