Regletas de Fracciones para Imprimir PDF

Regletas de Fracciones para Imprimir PDF. Imprimibles para trabajar las Fracciones. Juegos Matemáticos de Práctica de Fracciones. Ejercicios de Fracciones con regletas manipulables. Regletas Cuisenaire de fracciones. Barra de Fracciones. Tiras de Fracciones. Tiritas de papel para actividad de fracciones.

Utiliza la clave neoparaiso.com para abrir el PDF.

Explorar las matemáticas con una variedad de representaciones es realmente útil para los estudiantes. Las regletas de Cuisenaire son objetos manipulativos favoritos de los maestros. Tan potentes y versátiles. Además, nos ayudan a mover a los estudiantes de la fase de razonamiento de conteo al pensamiento aditivo y luego del razonamiento aditivo al multiplicativo.

El material didáctico "Regletas" apoya al alumno de primero de primaria para que sea capaz de:

Comparar números cardinales u ordinales por lo menos hasta el 10.
Resolver y modelar problemas de suma y resta utilizando los signos +, -, =.
Resolver problemas de adición y sustracción con distintos significados usando números dígitos.
Resolver problemas que impliquen identificar relaciones entre los números.
Solucionar mentalmente problemas de suma y resta con múltiplos de 10 menores que 100.

George Cuisenaire, un maestro de primaria en Thuin, Bélgica, tuvo la idea de crear las regletas como un medio de enseñanza para sus alumnos. A lo largo de varias décadas, éstas se han convertido en materiales didácticos esenciales en la enseñanza de las matemáticas.

El uso de regletas permite abordar temas como las cuatro operaciones básicas, fracciones, área, volumen, raíces cuadradas, resolución de ecuaciones simples, sistemas de ecuaciones e incluso ecuaciones cuadráticas.

Al manipular las regletas los estudiantes descubren, por medio de su propia experiencia, nociones o conceptos ligados a las características físicas de las mismas. De este modo, ellos recurren a sus propios razonamientos, facultades y creatividad, logrando una interiorización de los conocimientos.

El material consta de un juego de regletas de varios tamaños y colores. Cada tamaño está asociado a un color y un número. La longitud de las regletas varía. Y pueden tener o no tener ningún tipo de marca y permiten estimular la capacidad de memoria y relación de conceptos aparentemente no vinculados entre sí, como cantidad, color y longitud.

A través de las actividades propuestas en guías se trabajarán diferentes conceptos y problemas de una forma totalmente lúdica que resulte atractiva para los estudiantes. Asimismo, el docente podrá hacer uso de su creatividad y conocimientos para encontrar diferentes usos del material y así diseñar nuevas actividades.

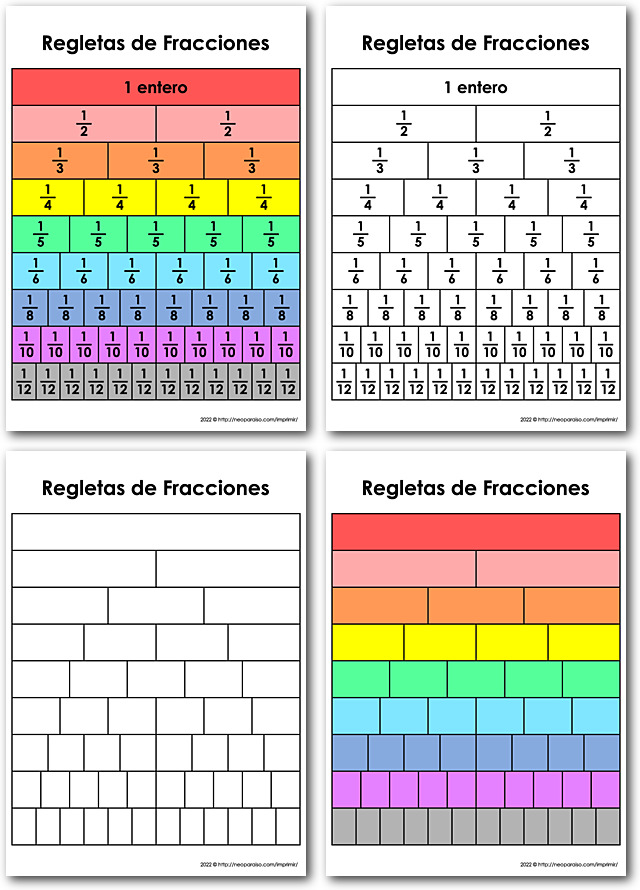
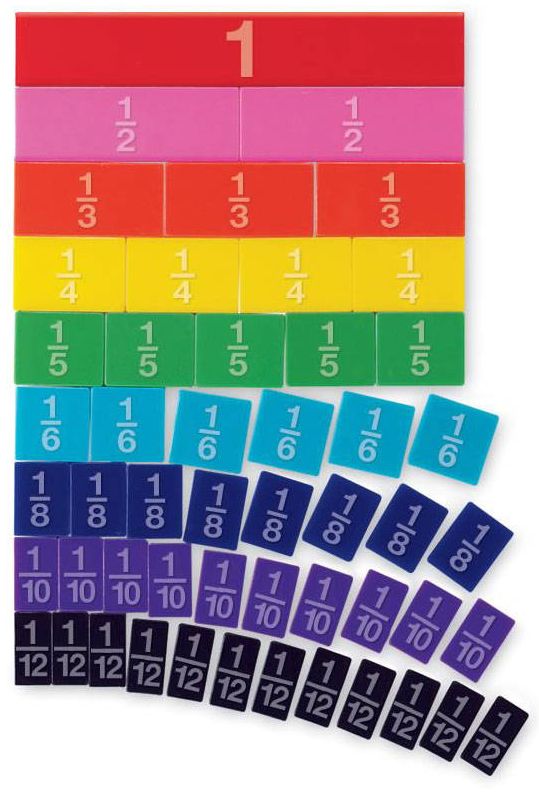
Las regletas de fracciones, también llamados barras de fracciones o tiras de fracciones, son un material educativo manipulable más importante que puede tener para enseñar fracciones. Son rectángulos de plástico (o cartulina plastificada) de colores brillantes que representan un todo, mitades, tercios, cuartos, quintos, sextos, octavos, décimos y doceavos. Cada regleta usa el entero del mismo tamaño. Incluso puede comprar regletas de fracciones marcados con equivalentes decimales. Mientras que otros objetos manipulables, como las varillas de Cuisenaire y los bloques de patrones, también son excelentes para desarrollar la comprensión de cómo funcionan las fracciones, las fichas son necesarias.

Según la revista The Scientific American, el conocimiento de fracciones de los estudiantes de quinto grado predice el aprendizaje de álgebra y el rendimiento general en matemáticas de los estudiantes de secundaria... y, sin embargo, los estudiantes de sexto y octavo grado responden correctamente a las preguntas sobre operaciones con fracciones solo la mitad de las veces.

Las habilidades que puede enseñar directamente mediante el uso de regletas de fracciones incluyen comparar y ordenar fracciones, números mixtos, encontrar denominadores comunes, fracciones equivalentes y todas las operaciones con fracciones, así como proporciones. La clave está en hacer preguntas y guiar a los niños para que vocalicen los patrones que ven. Comenzarán a ver relaciones y a descubrir "trucos" por sí mismos. Entonces, no solo ya no necesitarán los objetos manipulables, sino que comprenderán cómo y por qué funcionan las matemáticas.

1. Regletas de fracciones creadas por estudiantes

Si bien se pueden adquirir las regletas de fracciones prefabricadas, por cuestiones de costa tambíen los estudiantes pueden hacer las suyas. La práctica cinestésica ayuda a profundizar la comprensión y crear memoria a largo plazo. También les permite a los estudiantes tener su propio conjunto de manipulables que pueden tener con ellos para usar durante el tiempo libre o en casa. Recomiendo que los niños creen durante la instrucción en grupos pequeños para que pueda asegurarse de que sus cortes y proporciones sean correctos; si hacen sus tiras incorrectamente, la lección hará más daño que bien. Otra opción es hacer que los estudiantes usen plantillas como esta . Sus tiras serán precisas, pero el aprendizaje no es tan profundo como cuando diseñan las suyas.

Para encontrar fracciones equivalentes se puede usar "regletas de fracciones", que son una forma gráfica de representar las fracciones.

Elabora regletas en casa según el molde. Hazlo con ayuda de un familiar, puedes usar cartón grueso, material microporoso o algún otro material resistente:

Colorea según se indica.
Recorta cada sector.
Colócalo en un recipiente para que puedas jugar.

2. Fracciones Equivalentes con Regletas

Los objetivos de la lección son:

entender que las fracciones son parte de un todo
encontrar relaciones entre fracciones
encontrar fracciones equivalentes (diferentes fracciones que equivalen a la misma cantidad. Ej. 1/2 = 2/4)

Se comienza modelando cómo encontrar relaciones entre fracciones, moviendo mis tiras de fracciones y colocando diferentes combinaciones de fracciones una al lado de la otra.

Una vez que los estudiantes comprendan de forma básica cómo encontrar fracciones equivalentes, se les pone la tarea de acumular tantas fracciones equivalentes como pudieran encontrar.

Los alumnos se pueden mover libremente por su área de trabajo, extendiendo sus tiras de fracciones sobre las mesas y en el piso.

Comparan fracciones mientras se busca la equivalencia, varios sets de regletas una al lado de otra, que midan lo mismo.

¿Cuántas fracciones equivalentes diferentes puedes encontrar?

3. Multiplicación de Fracciones con Regletas

4. División de Fracciones

Dividir fracciones puede ser muy difícil para muchos estudiantes. Es difícil visualizar dividir una fracción en grupos de otras fracciones. Para dividir fracciones, muchos estudiantes memorizan el algoritmo saber por qué funciona.

Sin una comprensión conceptual de la división de fracciones, los estudiantes tienden a quedarse atascados cuando se encuentran con problemas (especialmente problemas verbales) en los que tienen que dividir por fracciones no unitarias como 2/3 o 3/4, o problemas en los que el divisor es mayor que el dividendo

Puede ayudar a sus alumnos a comprender cómo dividir fracciones usando tiras de fracciones que pueden mover. Los objetos manipulables y las representaciones visuales son estrategias basadas que apoyan el aprendizaje de nuevos conceptos matemáticos. Las tiras de fracciones pueden ayudar a los estudiantes no solo a comprender el concepto de dividir fracciones, sino también a ver literalmente cómo resolver estos problemas sin tener que hacer ningún cálculo.

Objetivo: Los estudiantes usarán regletas de fracciones para mostrar y resolver la división de dos fracciones.

Cómo preparar:

Reunir y explorar materiales. Entregue a cada estudiante o pareja de estudiantes un juego de tiras de fracciones. Pida a los alumnos que corten cada tira en fracciones unitarias (con un numerador de 1). Para los estudiantes que luchan con las habilidades motoras finas, considere tener algunos conjuntos ya recortados. También puede hacer algunos juegos de cartulina o plastificados para estudiantes.

Después de cortar cada tira en fracciones unitarias, pida a los estudiantes que vuelvan a armar cada una de las tiras para que tengan un conjunto completo que coincida con lo que está en el imprimible. Entregue a los estudiantes una copia del imprimible o proyecte una imagen del imprimible para que tengan un modelo visual al que referirse.

Una vez que los estudiantes hayan ordenado todas las tiras, vuelva a introducir el concepto de un todo. Recuerde a los estudiantes que la representación visual de 1 y la palabra "todo" a menudo son intercambiables cuando hablamos de fracciones.

Diga: "En la parte superior de la página tenemos 1 entero completo". Luego, pregunte a los estudiantes qué notan sobre las tiras debajo de la pieza entera. Modele un ejemplo. Podría decir: "Me doy cuenta de que cada fila de tiras de fracciones tiene el mismo tamaño". Pida a los estudiantes que compartan lo que notan con un compañero. Luego pida a algunos alumnos que compartan con toda la clase. Recuerde a los estudiantes las lecciones anteriores en las que trabajaron en la división de números enteros por fracciones.

Como enseñar:

1. Repasar dividir un número entero por una fracción. Pida a los alumnos que coloquen una tira completa en la parte superior de su escritorio. Debajo de esa tira, pida a los estudiantes que coloquen tantas tiras de 1/4 como sea necesario para que coincidan con el mismo tamaño que 1 entero. Escriba la ecuación 1 ÷ 1/4 = 4 en la pizarra y pregunte a los alumnos cómo saben que esto es cierto. Los estudiantes deben referirse a las tiras que tienen delante para explicar la respuesta.

Revise todas las formas comunes en que los estudiantes podrían explicar sus respuestas proporcionando los siguientes ejemplos, tanto visual como verbalmente:

"1/4 cabe en 1 entero 4 veces"
"Hay 4 grupos de 1/4 en 1 entero"
"1 dividido en grupos de 1/4 es 4"
"4 por 1/4 es igual a 1"

2. Explique cómo usar tiras de fracciones para dividir una fracción entre una fracción. Use el modelo "Yo hago, nosotros hacemos, tu haces" (también conocido como modelo de instrucción de liberación gradual) para guiar a los estudiantes a través del proceso de uso de las regletas o tiras.

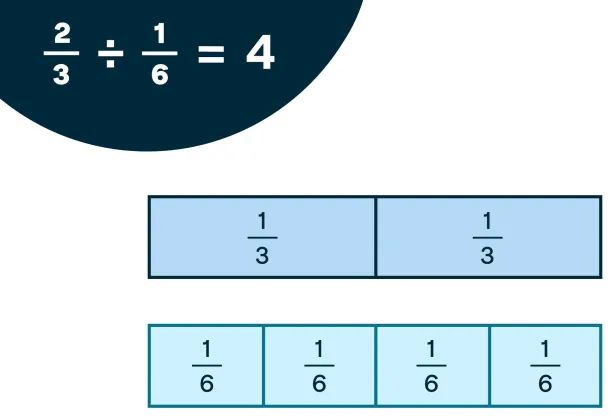
Yo hago: Explique y modele usando las tiras. Diga, "Ahora podemos usar una estrategia similar para resolver problemas de división con dos fracciones en ellos. Echemos un vistazo a 1/2 ÷ 1/6. Comenzaré colocando una tira de 1/2 en la parte superior como esta. Luego, debajo, colocaré tantas tiras de 1/6 como pueda para que coincida con la tira de 1/2. Podemos ver que se necesitan una, dos, tres tiras de 1/6 para que coincida con la tira de 1/2. Así que puedo concluir que 1/2 ÷ 1/6 = 3, o 1/6 encaja en 1/2 tres veces".

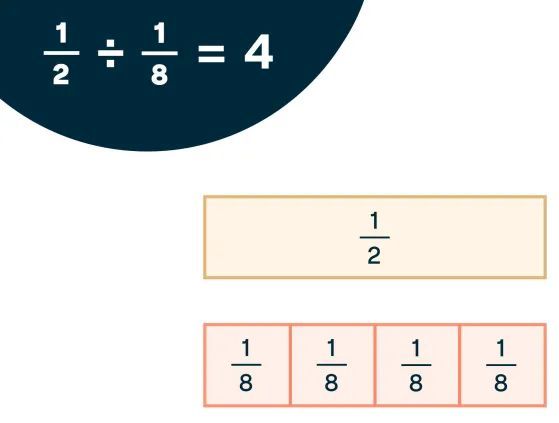
Lo hacemos: Guíe a los estudiantes para que lo prueben con usted. Diga, "Ahora probemos esto juntos. Comience con 1/2 de nuevo. Colocaré 1/2 en la parte superior. Ustedes hagan lo mismo." Modelo colocando la 1/2 tira en la parte superior. "Esta vez divide 1/2 entre 1/8. Coloquemos tantas tiras de 1/8 como podamos para que coincidan con la tira de 1/2". Modele y luego camine para ayudar a los estudiantes que puedan necesitar apoyo. Para los estudiantes que pueden configurarlo correctamente, pídales que escriban el problema de división con la solución.

Una vez que todos hayan terminado, discuta la respuesta como clase. Escriba la oración numérica de división para los estudiantes que quizás no hayan obtenido la respuesta correcta. Describe la solución de varias maneras.

1/8 cabe en 1/2 cuatro veces

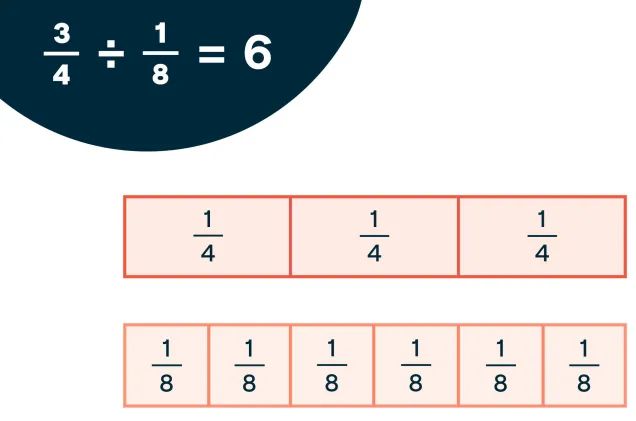
4.1. Otros ejemplos

4.2. Por qué funcionan las tiras de fracciones

Las tiras de fracciones (o barras o regletas de fracciones) ayudan a los estudiantes a ver que el mismo "entero" se puede dividir en diferentes partes del mismo tamaño. Cuando los estudiantes mueven las tiras y las colocan una al lado de la otra, pueden visualizar las cantidades fraccionarias. También pueden hacer comparaciones entre fracciones y hacer sumas, restas, multiplicaciones y divisiones con fracciones.

Los estudiantes que experimentan dificultades con las matemáticas, particularmente con las fracciones, a menudo tienen problemas para conectar el significado de los números y símbolos en un algoritmo. Las tiras de fracciones dan a los estudiantes una representación conceptual del problema. Pueden usar las tiras para crear tanto el dividendo como el divisor para que puedan verlos como partes fraccionarias de un todo. Los estudiantes también pueden contar el número de grupos (el cociente) que se forman al dividir.

Con esta estrategia, usa instrucciones en el modelo "Yo hago, nosotros hacemos, tú haces". Al mostrarles a los estudiantes cómo usar las tiras de fracciones y luego permitirles practicar con el apoyo del maestro y de sus compañeros, esta estrategia brinda múltiples oportunidades de aprendizaje.

5. Juego de Colorear Fracciones

Jugadores: 2 o más

Edades: A partir de 8 años

Ideas matemáticas: Equivalencia, fracciones, suma, descomposición

Preguntas para hacer:

¿Qué fracción obtuviste? ¿Qué otras fracciones podrías completar que serían equivalentes?
¿De cuántas maneras puedes llenar 1/2 en el papel? ¿De cuántas maneras puedes completar 2/2?
¿Qué crees que significa 3/2?

Para jugar a Colorear Fracciones, deberá imprimir una hoja de de fracciones sin color y sin números para cada jugador. La hoja del juego contiene una pared de fracciones en blanco, que es una representación muy común de las fracciones. Cada fila es un conjunto diferente de fracciones que equivalen a una unidad. Tienes dos mitades, tres tercios, cuatro cuartos, y así sucesivamente.

También necesitará un par de dados etiquetados de la siguiente manera:

Dado uno: 1, 2, 2, 3, 3, 4
Dado dos: ⊗/2, ⊗/3, ⊗/4, ⊗/6, ⊗/8, ⊗/12

El primero dado indica el numerador de tu fracción, mientras que el segundo dado te dice el denominador. Entonces, si sacas 2 y */6, tu fracción es 2/6.

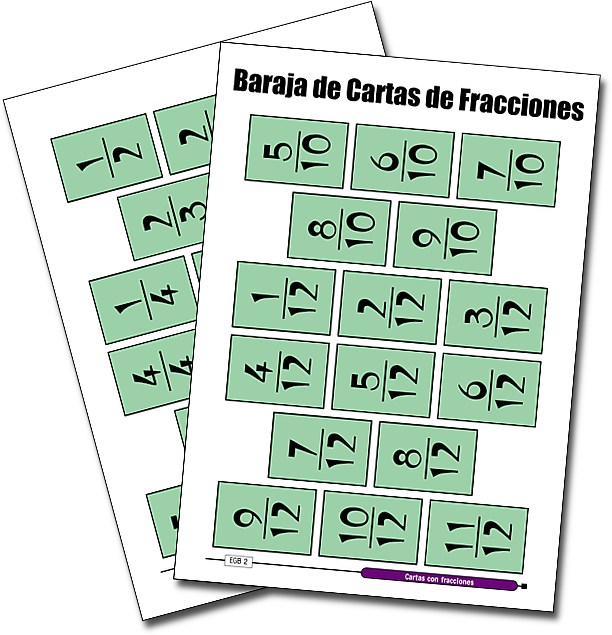
(Si no tiene dados en blanco y marcadores disponibles, puede imprimir y barajar estas cartas de fracciones, y escoger las que contentan las mismas fracciones)

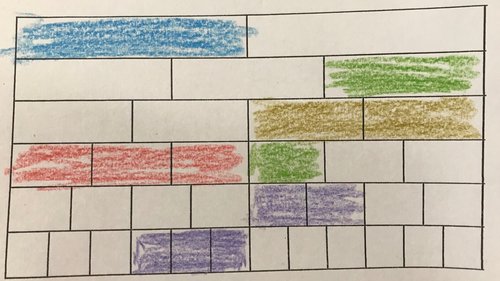
Cada jugador tira los dados y luego tiene que colorear una porción de su pared de fracciones que sea equivalente a esa fracción.

Entonces, si saca 1/2, puede colorear 1/2, o puede colorear 2/4 o 3/6 o 4/8 o cualquier otra cosa que tenga la misma longitud que 1/2. Incluso puedes combinar fracciones de diferentes tamaños: si quieres colorear 1/3 y luego 1/6, ¡puedes hacerlo! Esas fracciones se combinan a 1/2. Puede ver varias formas de colorear en 1/2 en la imagen a continuación.

$Imagen: juego colorear fracciones ejemplo1$

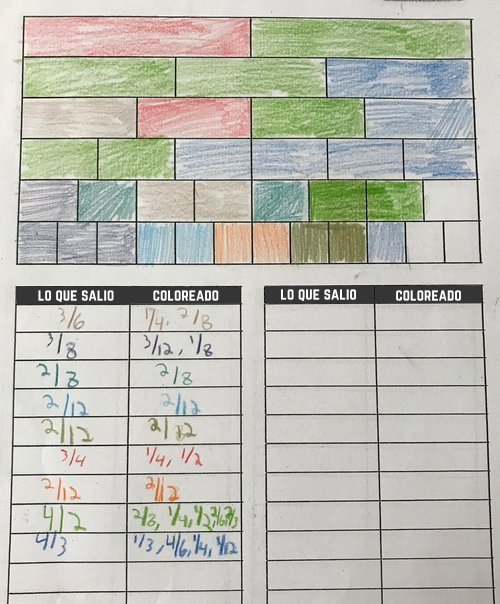
Así que digamos que tiras 1/2 y decides sombrear 1/4 y 2/8. Con un lápiz de color o marcador, coloreas tus fracciones. Luego, escribe "1/2" como lo que tiraste y "1/4 + 2/8" como lo que coloreaste.

$Imagen: juego colorear fracciones ejemplo2$

Este paso, que es extremadamente importante, hace que los niños piensen en las formas en que las fracciones se pueden combinar usando la suma para hacer fracciones más grandes. Volveremos a eso más tarde...

De cualquier manera, el otro jugador toma un turno para tirar los dados y sombrear sus propias fracciones. Si no puede sombrear su fracción o una fracción equivalente por algún motivo, debe pasar. La primera persona en completar todo su tablero es el ganador.

5.1. ¿Dónde está la matemática?

Me encanta este juego porque hay mucho de qué hablar, ya seas de tercer o octavo grado.

Una de las ideas centrales del juego son las fracciones equivalentes. Los niños pasan años buscando y simplificando fracciones equivalentes, pero rara vez la conexión entre 2/3 y 4/6 se hace visualmente clara en años posteriores.

Pero en el juego de Colorear Fracciones, puedes ver claramente que 4/6 tiene exactamente la misma longitud que 2/3 y, por lo tanto, es otra forma de describir la misma cantidad de espacio.

Además, los niños ocasionalmente sacarán fracciones mayores que 1, como 3/2 o 4/3. Esta puede ser incluso la primera vez que ven una fracción con un numerador que es mayor que el denominador. ¿Está eso siquiera permitido? ¿Cómo puedes sombrear cuatro tercios si solo tienes tres tercios en la pared de fracciones?

La belleza del juego es que la pared de fracciones crea un andamiaje visual para estas conversaciones. Los niños pueden comparar longitudes para encontrar la equivalencia. Entonces podrían darse cuenta de que 3/3 es simplemente un todo, lo que significa que pueden sombrear una fila completa para representar esa cantidad. Y dado que cada fila tiene la misma longitud, pueden sombrear 12/12 u 8/8 con la misma facilidad que 3/3.

5.2. Preguntas que hacer sobre la actividad

La primera pregunta que debe hacerse es lo más importante del juego: "Veo que salió 2/3. ¿De qué otras formas pueden colorear esa longitud de fracción? "

El juego de fracciones es un juego que se beneficia de las jugadas repetidas, así que No se moleste si sus niños tienden hacia las soluciones más fáciles al principio. La estructura del juego, con su conjunto cada vez menor de fracciones disponibles, los alentará a pensar creativamente con el tiempo.

También puede invertir la pregunta: pídales que confirmen sus propias decisiones: "Saqué 1/2, así que voy a colorear 1/4 y 1/6. ¿Está bien?"

Si identifican correctamente el error, ¡pídeles que expliquen por qué! Cuanto más tiempo pasan justificando su razonamiento y describiendo fracciones en voz alta, más profundamente interiorizan las principales lecciones que ofrece el juego.

Si eres una maestra que usa esto en un salón de clases, puedes convertir la tabla de fracciones de cada persona en un conjunto de problemas para probar. "Ok, María llenó 1/3 y 1/6 y dice que es igual a 1/2. ¿Pueden todos usar lo que hemos aprendido sobre la suma de fracciones para demostrar que tiene razón?"

Una vez que sus niños se sientan más cómodos con el juego, ¡puede convertirlo en un rompecabezas! Pregúnteles "¿De cuántas maneras únicas podemos sombrear 1/2?" Esto, por cierto, es una actividad muy divertida para probar por tu cuenta. ¡Combine sus propios métodos con las ideas de sus niños para ver cuántos pueden crear juntos! Luego pídales que sugieran la siguiente fracción y encuentre todas las formas de completar esa cantidad.