Juegos Matemáticos de Cartas

Mazo de Cartas Francesas para cortar. Naipes parar Imprimir. Juegos de cartas para imprimir. Secuencia "juegos con cartas" donde se trabaja juego reglado reconocimiento de número y colecciones. Baraja de Naipes Gratis. Cartas Tradicionales para descargar. Qué juegos hay para matemáticas con cartas regulares. Juegos de sumas para niños.

Utiliza la clave neoparaiso.com para abrir el PDF.

Contenido

1. Juegos Matemáticos de Cartas

¿Se te dificulta a ti a tus niños memorizar resultados matemáticos? Los juegos de naipes valen más que mil hojas de trabajo de prácticas, permitiéndote desarrollar la velocidad de cálculo de los niños de una manera que no produce estrés ni requiere pruebas.

Aquí encontrarás varios juegos matemáticos diferentes (incluyendo variantes) que no necesitan mucho más que un mazo de cartas corrientes. Son preferidos por muchas maestras ya que:

• las barajas son baratas, ya que las barajas de cartas son un sistema de juego tradicional, se producen de manera masiva y hay mucha oferta de ellas, por lo que tienen bajo precio
• son fáciles de conseguir, ya que son utilizadas también para pasar el tiempo o reuniones de amigos, son populares y se encuentran fácimente en papelerías
• son portables, no pesan mucho ni ocupan mucho espacio, una maestra puede llevar varios mazos y permitir que varios grupos de niños puedan estar involucrados en la actividad simultáneamente
• no requieren preparación, permiten pasar más tiempo realizando la actividad de aprendizaje, que preparando tableros o artilugios.
• son versátiles, pueden ser utilizadas para una amplia variedad de actividades matemáticas, como juegos de contar, comparar números, practicar operaciones aritméticas, entender conceptos de probabilidad, entre otros.

Las cartas son una herramienta pedagógica eficaz para enseñar matemáticas debido a su versatilidad, accesibilidad, interactividad y aplicación práctica en el desarrollo de habilidades matemáticas.

2. Guerra Básica

Conceptos matemáticos: menor que, mayor que, suma, resta multiplicación, división, fracciones, números negativos, valor absoluto, resolución de problemas en varios pasos.

MATERIALES

Necesitarás varios mazos de cartas matemáticas. No te apures a buscarlas en la tienda de materiales escolares ni trates de pedirlas a través de tu catálogo favorito. Las cartas matemáticas son cartas normales a las que se les ha quitado, las J, Q, K y comodines.

Haz un mazo de cartas por cada jugador. Un mazo matemático contiene 40 cartas, así que un solo juego de Guerras de Sumas permite al niño resolver 20 problemas, y él escucha a su oponente resolver 20 más, y si tus niños son como los míos, es poco probable que quieran parar el juego al terminar con las cartas.

NOTAS

Mientras tus estudiantes memorizan los resultados aritméticos, es posible que necesiten práctica extra con los que son más difíciles como 6 × 8. Sin embargo, con un mazo regular, he visto que aparecen demasiados problemas como 1 × 9 o 2 × 7. Para dar un reto mayor para niños de más edad, haz para cada jugador un mazo doble de cartas, pero retirando los aces, los dos, y los diez. Esto da a cada jugador mazos de 56 cartas con los problemas más difíciles de calcular.

REGLAS

Cada jugador toma su mazo de cartas, todas tapadas, y destapa una carta. El jugador con el número mayor gana la batalla, ubicando su carta y las cartas capturadas en la pila de los prisioneros. Siempre que haya un empate por la carta mayor, todos los jugadores batallan: cada jugador saca tres cartas tapadas y una destapada. La mayor de estas nuevas cartas destapadas captura todo lo que está en la mesa. Ya que todos los jugadores participan, alguien que tenía una carta baja en el primer choque podría, a fin de cuentas ganar la batalla. Si ocurre un empate nuevamente, se repite el patrón de batalla de 3 tapadas y 1 destapada hasta que alguien rompa el empate. El jugador que gane la batalla captura todas las cartas jugadas en ese turno.

FIN DEL JUEGO

Cuando los jugadores han batallado hasta acabar todo el mazo, se cuentan los prisioneros. Quien sea que haya capturado la mayor cantidad de cartas gana el juego. Alternativamente se pueden barajar las cartas obtenidas por cada jugador y continuar el juego hasta que alguien obtenga una cantidad de prisioneros tan grande que los otros jugadores se rindan.

VARIACIONES

• En la variación más popular, el patrón básico de 3-tapadas-1-destapada se reemplaza por 2-tapadas-2-destapadas. Jugando independientemente cada pareja de cartas destapadas.
• Otra alternativa es la siguiente: en caso de empate, las cartas son colocadas en una pila central. La siguiente batalla se juega normalmente, sin sacar cartas tapadas, y el ganador de esa batalla se lleva la pila central también.

3. Guerras matemáticas específicas

Juego de Sumas

Los jugadores voltean dos cartas por cada batalla. La suma mayor gana.

Juego de Sumas Avanzada

Voltea tres (o cuatro) cartas por cada batalla y súmalas todas.

Juego de Restas

Los jugadores voltean dos cartas y restan la menor de la mayor. Esta vez, la mayor diferencia gana la batalla.

Juego de Multiplicaciones

Cada cual voltea dos cartas y las multiplica.

Juego de Multiplicaciones Avanzada

Voltea tres (o cuatro) cartas por cada batalla y multiplícalas.

Juego de Fracciones

Los jugadores voltean dos cartas y hacen una fracción, usando la carta menor como el numerador. La fracción mayor gana la batalla.

Juego de Fracciones Impropias

Voltea dos cartas y haz una fracción, usando la carta mayor como numerador. La fracción mayor gana.

Juego de Sumas con Negativos

Las cartas negras son números positivos; las cartas rojas son números negativos. La suma mayor gana. Recuerda que -2 es mayor que -7.

Juego de Multiplicaciones con Negativos

Las cartas negras son números positivos; las cartas rojas son números negativos. El producto mayor gana. Recuerda que dos números negativos crean un producto positivo.

Guerra Salvaje

Los jugadores voltean tres cartas y pueden hacer cualquier operación matemática que quieran con los números. La respuesta mayor gana la batalla.

Guerra Salvaje Avanzada

Las cartas negras son números positivos; las cartas rojas son números negativos. Los jugadores voltean cuatro cartas (o cinco) y pueden hacer cualquier operación matemática que quieran con los números. La respuesta mayor gana la batalla.

Guerra Salvaje Inversa

Los jugadores voltean tres cartas (o cuatro, o cinco) y pueden hacer cualquier manipulación matemática que deseen con los números. La respuesta con el menor valor absoluto (más cercano a cero) gana la batalla.

4. Juego 31

Autor

• Juego 31 proviene del libro clásico del matemático británico Henry Dudeney, The Canterbury Puzzles.

Conceptos matemáticos

• suma hasta treinta y uno, pensar en el futuro.

Jugadores

• mejor para dos.

Material

• una baraja de cartas solo se usa del As al 6

Reglas

Coloque el as al seis de cada palo en fila, boca arriba y sin superponerse, un palo encima del otro, es decir formando una tabla de de 4x6. Tendrás una columna de cuatro ases, una columna de cuatro dos, y así sucesivamente: seis columnas en total.

El primer jugador voltea una carta boca abajo y dice su valor numérico. Luego, el segundo jugador voltea una carta boca abajo, la suma al número del primer jugador y dice la suma.

Los jugadores se alternan, cada vez voltean una carta, suman mentalmente su valor al total acumulado y dicen la nueva suma en voz alta. El jugador que llegue exactamente a treinta y uno, o que obligue al siguiente jugador a superar esa suma, gana el juego.

VARIACIONES

• En lugar de poner las cartas en orden revolverlas antes de formar la tabla (así que los niños deban mirar bien para ver qué números quedan).
• Jugaron al revés, contando desde 31 a 0, usando la resta.
• Para un juego más corto, utilice sólo el as al cuatro de cada palo. Juega con una suma objetivo de 22.
• O jueguen hasta el 22, pero no sumen los números de los demás. Deje que los jugadores mantengan sus propios totales acumulados por separado.

5. Veinte-Veinte

Autor

• KAMII, C. Reinventando la aritmética II, Madrid: Visor, 1989

Nivel

• Final del Ciclo Inicial y principio de Ciclo Medio de Primaria.

Material

• Una baraja de cartas del 1 al 10 x 4 = 40 cartas sin figuras.
• Más 6 fichas (tipo parchís) para cada jugador o equipo. Un color distinto para cada jugador.

Nº de jugadores

• De 2 a 4 jugadores o equipos.

Reglas

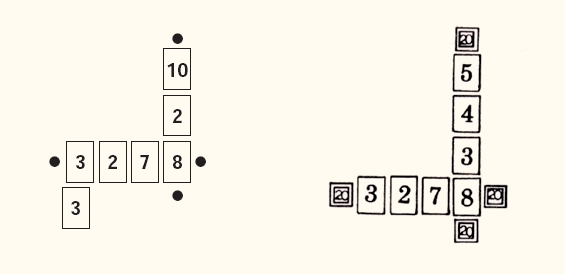
Cada jugador tiene seis fichas y se le reparten 5 cartas. Por turnos, cada jugador coloca una carta encima de la mesa al lado de otra (ver figura). Después coge una carta del montón para volver a quedarse con 5. Cuando un jugador coloca una carta que suma 20 en una fila o columna, cierra esta hilera con una ficha en cada extremo (o sea dos). Gana el primer jugador que ha colocado sus seis fichas.

Contenidos matemáticos

• Números naturales del 1 al 20.
• Cálculo mental.
• Suma encadenada de varios sumandos.
• Descomposición del 20 en varios sumandos.
• Noción de complementario.

Este juego permite desarrollar distintas capacidades a la vez. Por un lado, requiere utilizar estrategias de cálculo mental para sumar rápidamente las cifras ya colocadas; luego, buscar el complementario a 20 y comprobar si se posee o no. También posibilita pensar o preparar jugadas que impliquen más de una tirada, o incluso tener preparadas varias posibilidades de actuación en un mismo momento. En este juego es tan importante intentar ganar, es decir, buscar la combinación que me favorezca, como intentar entorpecer al contrario. Así pues, todas estas habilidades que se desarrollan en este juego, en realidad, favorecen el pensamiento lógico, la creatividad y aumentan la capacidad para resolver problemas.

6. Casillas para neutralizar

Autor

• Talleres y Juegos Matemáticos, Ayuntamiento de ASPE

Nivel

• Educacion Primaria Segundo Ciclo

Nº de jugadores

• Dos o cuatro jugadores por parejas

Objetivos matemáticos

• Realizar operaciones básicas sencillas.
• Expresar un número como suma o diferencia de otros dos.

Material

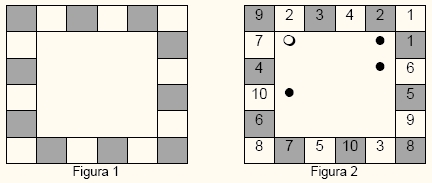
• Un casillero como el de la figura 1.
• Dos series de cartas del 1 al 10 de diferentes palos

Reglas

Se pretende neutralizar el mayor número de cartas del jugador contrario. Una carta está neutralizada por dos del contrario si estando situada entre estas dos, la suma o la diferencia de ambas da como resultado el número que figura en la carta central.

Cada jugador dispondrá de una colección de cartas. Uno jugará sobre las blancas y otro sobre las negras.

Cada jugador, por turno, colocará una de sus cartas sobre una casilla libre de su color. Cuando todas las cartas estén colocadas se procede a la puntuación: si dos cartas neutralizan una del adversario, el jugador que neutraliza se apunta un tanto.

El vencedor es el que acumule más puntos. En la figura 2 el jugador de blanco neutraliza el número negro 9 ya que está rodeado por los números blancos 2 y 7 (cuya suma es 9).

El jugador negro neutraliza el número blanco 1 ya que está rodeado por los números negros 2 y 1 (cuya resta es 1). Neutraliza el número 6, porque está rodeado por los números negros 1 y 5. Y finalmente neutraliza el número 10 porque está rodeado por los números 4 y 6.

7. Saludo

Objetivos matemáticos

• Operaciones: suma/resta juntas o multiplicación/división juntas

Materiales

• Necesitas una baraja de cartas estándar sin comodines ni figuras. Las cartas As tienen un valor de uno.

Nº de jugadores

• 3 jugadores

Reglas

• Los jugadores se turnan para ser el "juez". Los otros dos jugadores toman cada uno una carta del mazo, sin mirarla.
• El juez dice "saluden" y los demás jugadores sostienen la carta frente a sus frentes para que mire al otro jugador y no puedan verla ellos mismos.
• Luego, el juez suma (o multiplica) en silencio los dos números mentalmente y les dice la respuesta a los demás jugadores.
• Los jugadores usan lo que saben sobre el número de su compañero para descubrir el número en su tarjeta y decirlo.
• La primera persona que diga su carta correctamente gana esa mano y se queda con la carta.
• Los roles rotan y se repiten hasta que se acaben todas las cartas. El ganador tiene la mayor cantidad de cartas al final del juego.

8. Enfrenta los hechos

(Variante de Saludo pero para 4 jugadores)

Materiales

• Una calculadora
• Una baraja de cartas estándar sin comodines ni figuras. Las cartas As tienen un valor de uno.

Nº de jugadores

• 4 jugadores

Reglas

• Los jugadores A y B se sientan uno frente al otro. Cada uno tiene la mitad de la baraja. Una tercera persona, el que llama, se sienta al lado que mira hacia el centro.
• Cuando esta persona dice "Saluden", los dos jugadores con las cartas toman cada uno la carta superior sin mirarla y la colocan en sus frentes para que los demás puedan verla. La persona que llama dice "La suma es ___". (o producto)
• Los jugadores A y B intentan cada uno calcular el número que tienen ellos mismos. El jugador que nombre correctamente su propio sumando/factor primero se quedará con ambas cartas y las agregará al final del mazo.
• Un cuarto jugador, el "inspector", tiene una calculadora para comprobar las sumas/productos.
• Después de un tiempo determinado, gana la persona que tenga más cartas.

9. Haz 10

Objetivos matemáticos

• Complementos de 10 (o de otro número), suma, descomposición aditiva de números

Materiales

• Baraja de cartas sin las figuras.

Nº de jugadores

• 2-4 jugadores

Reglas de Haz 10

Objetivos matemáticos

• Complementos de 10 (o de otro número), suma, descomposición aditiva de números,

Reglas

• Reparte 12 cartas boca arriba.
• Los jugadores se turnan para encontrar y eliminar combinaciones de 10 (1 o más cartas a la vez). Cuando se retira una carta, reemplácela con una carta nueva del mazo.
• Cuando ambos jugadores estén de acuerdo en que no hay más decenas posibles, reparta 12 cartas más boca arriba sobre las cartas existentes.
• El ganador tiene la mayor cantidad de cartas al final del juego.

VARIACIONES

• Use tres tarjetas y sume hasta 20
• Use la multiplicación y productos sobre un número determinado
• Use la multiplicación de varios dígitos y encuentre productos mayores que 100.

10. Veo veo de multiplicación

Nivel: 3er de grado

Objetivos matemáticos

• Multiplicación. Este juego proporciona una gran práctica con las tablas de multiplicar
• Práctica de pensamiento flexible y la elaboración de estrategias

Nº de jugadores

• 2 jugadores

Materiales

• Retire las cartas con figuras (viejas) de una baraja de cartas regular. Distribuya toda la baraja de cartas boca arriba en una tabla de 8 X 5. Por ejemplo así:

Instrucciones

• Un jugador desafía al otro jugador a encontrar dos cartas una al lado de la otra, ya sea vertical u horizontalmente, que se multipliquen para crear un producto específico. Por ejemplo, podría decir: "Veo dos cartas con un producto de 36". Luego, el otro jugador busca dos cartas que se multiplican para dar 36 y puede recoger ese par junto con cualquier otro par que se multiplique para dar 36.
• Si el segundo jugador no logra ver algún par que se multiplique para dar el producto indicado, entonces el primer jugador puede reclamarlo. Los jugadores intercambian roles y continúan hasta que se despeja la mesa. El ganador es el jugador que tenga más cartas al final del juego.
• A medida que aparecen grandes espacios, el tamaño de la matriz se puede reducir para ayudar a llenar los espacios.

11. Oh no 99!

Si bien los estudiantes de primaria de mayor edad suelen estar aprendiendo números enteros más grandes, muchos todavía necesitan y se benefician de la práctica de la suma y resta mental de números pequeños. En este juego de cartas para dos personas, los jugadores intentan obligar a su compañero a ser quien eleve su puntuación conjuntamente acumulada por encima de 99.

Objetivos matemáticos

• El juego proporciona práctica para sumar y restar y, al mismo tiempo, brinda a los estudiantes la oportunidad de pensar estratégicamente.

Nº de jugadores

• 2 jugadores

Materiales

Carta	Valor
As	1 o 11
K	99
10	+10 or -10
J, Q	10
9	pasar
4	0, cambiar de dirección
Otras cartas	propio valor

Reglas

• Un jugador baraja las cartas y reparte cuatro cartas a cada jugador. Las cartas no repartidas permanecen en una pila, boca abajo.
• Los jugadores se turnan para jugar una carta a la vez, sumando o restando el valor de su carta a la puntuación acumulada conjuntamente.
• Cada vez que un jugador juega una carta, debe reemplazarla con la carta superior de la pila boca abajo.
• El juego continúa hasta que un jugador obliga a su compañero a superar la puntuación de 99.

ESTRATEGIA

Mientras el juego continúa, el total nunca supera los noventa y nueve. Los jugadores usan sus cuatros, que invierten la dirección del juego, sus dieces, que pueden sumar o restar diez del total y sus nueves, que les permiten pasar en su turno, para mantener el juego vivo después de que se juega una K, o si el total ya es muy alto.

Si el jugador se olvida de escoger una carta del mazo antes de que el siguiente jugador la haya descartado, el grupo grita "lero, lero" y ese jugador tiene que jugar el resto del juego con solo dos cartas.

CONSIDERACIONES PEDAGÓGICAS

¡Oh, no! 99! Proporciona un contexto en el que los estudiantes pueden practicar el cálculo mental. Durante el juego, los estudiantes suman repetidamente y ocasionalmente restan números entre 1 y 99.

Esto ciertamente les da la práctica que necesitan para volverse competentes y eficientes computacionalmente. Además, el juego motiva a los estudiantes. Aunque puede que no les entusiasme resolver docenas de problemas de cálculo sin contexto, en realidad eligen jugar ¡Oh, no! 99! incluso después de jugarlo varias veces en clase, los estudiantes todavía disfrutan del juego y están ansiosos por jugarlo durante el almuerzo o el momento de elección.

Además, el juego brinda a los estudiantes la oportunidad de utilizar el pensamiento estratégico mientras juegan. Los estudiantes deben considerar el valor de las cartas que tienen en la mano, formular hipótesis sobre qué cartas podrían tener sus compañeros y tomar decisiones basadas en sus ideas.

Finalmente, el juego proporciona un contexto en el que los estudiantes pueden realizar algún trabajo escrito. Sus escritos brindan información sobre cómo se comunican matemáticamente y cómo piensan acerca de descomponer números y unirlos. Es importante que los estudiantes tengan muchas oportunidades para practicar estas habilidades.

¿Es este juego demasiado fácil para los alumnos de quinto grado?

A primera vista, este es un juego fácil, pero contiene muchas matemáticas. Estudiantes jugando ¡Oh no! 99! practican el cálculo mental, utilizan el pensamiento estratégico y están expuestos a la probabilidad. Si fuera realmente demasiado fácil, los estudiantes perderían el interés con bastante rapidez. ¿Cuánto tiempo permanecería un grupo de alumnos de quinto grado involucrados en un rompecabezas de preescolar o en un episodio de Plaza Sésamo? Además, noté que varios alumnos de quinto grado usaban sus dedos para calcular los totales durante el juego. Esto sugiere que necesitan mucha más práctica con el cálculo mental. Si bien no prohíbo a los estudiantes contar con los dedos, trabajo con ellos para ayudarlos a avanzar hacia estrategias más eficientes. El juego, cuando se combina con una discusión sobre estrategias de cálculo, ofrece a los estudiantes oportunidades para ir más allá de los enfoques de "contar con". El juego también desarrolla el sentido numérico en los estudiantes que no dependen de sus dedos. Las estrategias que aprenden y fortalecen mientras juegan se pueden aplicar a problemas más grandes y desafiantes en el futuro.

Es útil tener un tablero de 100 para registrar qué número han alcanzado los jugadores. También ayuda a los estudiantes a sumar y reconocer patrones (por ejemplo, 10 más es el número debajo del último número y 9 más es como 10 más menos 1). Cuando los estudiantes descubren estos patrones por sí mismos, ¡los recuerdan mejor que si se los contamos!

LO MÁS DESCARGADO

Otros también vieron:

Cartas

Print and Play

Juegos

Operaciones Mixtas

Síguenos en Facebook

---