Fórmulas para resolver triángulos PDF

Fórmulas para resolver triángulos PDF gratis. Relaciones de los lados y ángulos. Cómo resolver triángulos generales. Ley de los senos. Ley de los cosenos. Aplicaciones de la trigonometría. Cómo encontrar los lados y ángulos que faltan en un triángulo. Usos prácticos de la trigonometría.

Fórmulas para Resolver Triángulos PDF

Utiliza la clave neoparaiso.com para abrir el PDF.

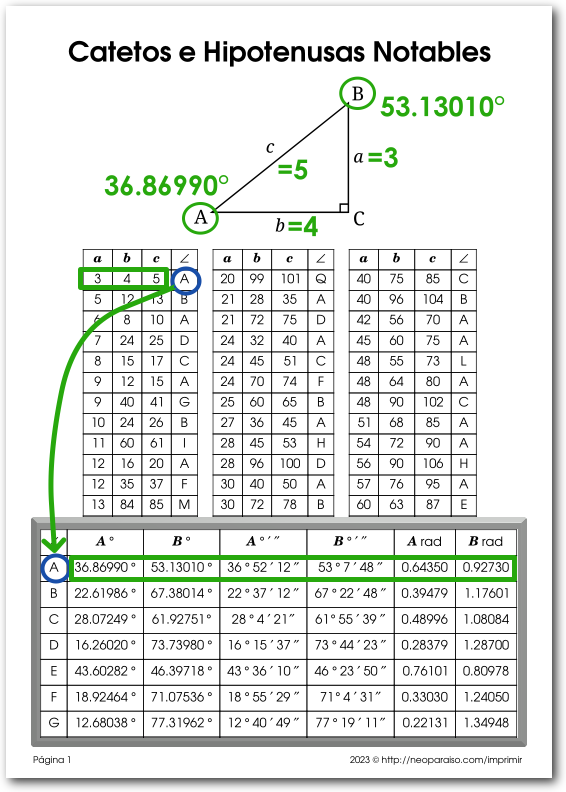
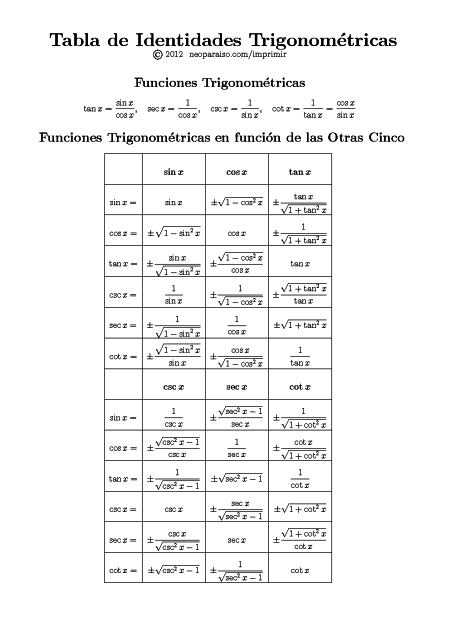
Una hoja que resume las fórmulas para resolver diferentes tipos de triángulos y encontrar sus ángulos y lados es una herramienta de referencia útil para estudiantes, profesores y cualquiera que trabaje con triángulos en diversos campos, como matemáticas, ingeniería, física o arquitectura. Así es como puede utilizar dicha hoja de referencia:

  1. Referencia rápida: la hoja de referencia proporciona una manera rápida y conveniente para varios métodos de resolución de triángulos. Cuando encuentre un problema de triángulo, puede consultar la hoja para identificar el tipo de triángulo y la fórmula adecuada a utilizar.
  2. Resolución de problemas: puede usarse para ayudarlo a resolver problemas de triángulos de manera más eficiente. Cuando tengas información conocida sobre un triángulo (por ejemplo, longitudes de los lados, ángulos), puedes usar las fórmulas de la hoja de referencia para determinar los lados o ángulos que faltan.
  3. Tareas y exámenes: los estudiantes pueden usar la hoja de referencia para verificar su trabajo en las tareas y prepararse para las pruebas y exámenes. Garantiza que utilicen las fórmulas y métodos correctos para resolver problemas relacionados con triángulos.
  4. Enseñanza y tutoría: los profesores y tutores pueden utilizar la hoja de trucos como ayuda didáctica para explicar los conceptos de resolución de triángulos a los estudiantes. Proporciona una descripción concisa de las fórmulas y principios esenciales.
  5. Tipos de problemas: la hoja se puede organizar para cubrir varios tipos de problemas, como encontrar lados faltantes, calcular ángulos, trabajar con triángulos especiales (por ejemplo, triángulos rectángulos) y tratar con diferentes tipos de triángulos (por ejemplo, escalenos, isósceles, equilátero).

Para qué se resuelve triángulos?

  1. Aplicaciones del mundo real: comprender cómo resolver triángulos es crucial en diversos campos como la ingeniería, la arquitectura, la física y la navegación. Por ejemplo, los arquitectos e ingenieros utilizan técnicas de resolución de triángulos para diseñar edificios, mientras que la navegación se basa en la comprensión de los triángulos para determinar posiciones y distancias.
  2. Trigonometría: Resolver triángulos es una aplicación fundamental de la trigonometría. Nos permite conectar ángulos y lados en triángulos usando funciones trigonométricas como seno, coseno y tangente. La trigonometría juega un papel fundamental en una amplia gama de aplicaciones científicas y de ingeniería.
  3. Habilidades para resolver problemas: aprender a resolver triángulos ayuda a desarrollar habilidades para resolver problemas. Le enseña cómo analizar situaciones geométricas complejas, aplicar principios matemáticos y encontrar soluciones sistemáticamente.
  4. Educación: Resolver triángulos suele ser parte del plan de estudios de matemáticas y campos relacionados. Es un concepto fundamental que ayuda a construir una base sólida para temas más avanzados en matemáticas y ciencias.

Una hoja de resumen para resolver triángulos [Documento en PDF] una herramienta valiosa para hacer referencia y aplicar las fórmulas relevantes de manera eficiente. Comprender cómo resolver triángulos es esencial no sólo con fines educativos sino también para aplicaciones prácticas en numerosos campos.