Tabla para Factorizar Trinomios de la forma x2 + bx + c
Utiliza la clave neoparaiso.com para abrir el PDF.
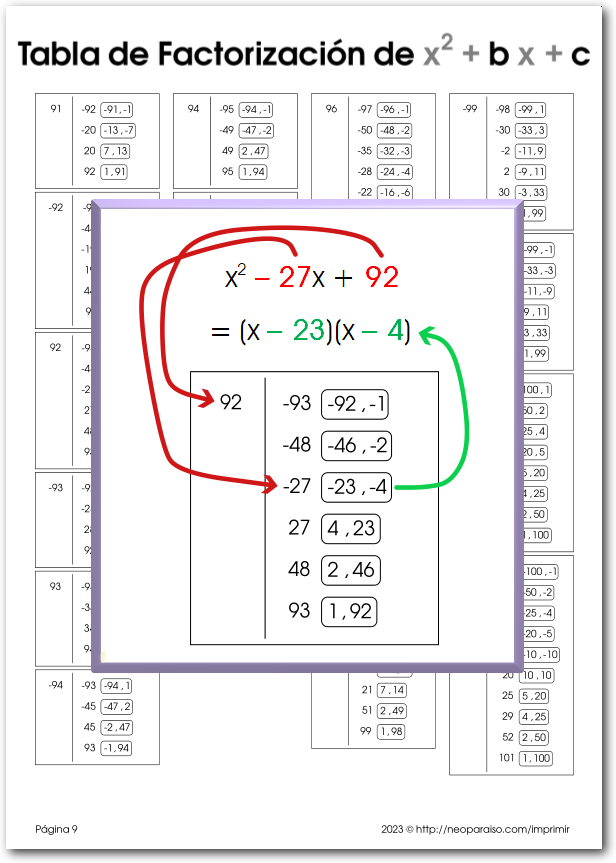
1. Cómo Factorizar Trinomios de la forma x2 + bx + c
Cómo factorizar trinomios de la forma x2 + bx + c puede ser un desafío para los estudiantes porque requiere que apliquen una variedad de técnicas y estrategias diferentes. Algunos de los principales desafíos que los estudiantes pueden encontrar al factorizar este tipo de polinomios incluyen:
- Encontrar los factores de c: Para factorizar un trinomio de la forma x2 + bx + c, los estudiantes necesitan encontrar dos números que se multipliquen a c y sumen b. Esto puede ser difícil si c es un número grande o poco conocido.
- Factorización de factores comunes: a veces, el trinomio puede tener factores comunes que deben factorizarse antes de factorizar la expresión cuadrática resultante.
- Identificación de casos especiales: Hay algunos casos especiales de trinomios, como los trinomios cuadrados perfectos y los trinomios de diferencia de cuadrados, que requieren técnicas especiales de factorización.
- Practicar aritmética mental: la factorización de trinomios a menudo implica realizar aritmética mental para encontrar los factores de c y determinar los signos de los factores.
- Aplicación de múltiples estrategias: la factorización de trinomios a menudo requiere la aplicación de múltiples estrategias, como prueba y error, agrupación o la fórmula cuadrática, hasta que se identifiquen los factores correctos.
Factorizar trinomios de la forma x2 + bx + c puede ser un desafío para los estudiantes, pero con práctica y perseverancia, pueden desarrollar las habilidades y estrategias necesarias para factorizar este tipo de polinomios con éxito.
Los estudiantes pueden usar esta tabla para factorizar trinomios de la forma x2 + bx + c porque proporciona un método simple para factorizar tales polinomios. La tabla contiene una lista de todas las combinaciones posibles de los coeficientes b y c y los números correspondientes de binomios factorizados. Al usar esta tabla, los estudiantes pueden identificar rápidamente los factores de un trinomio dado al encontrar la entrada correspondiente en la tabla.
Esta tabla es especialmente útil para los estudiantes que recién están aprendiendo a factorizar polinomios. Puede ayudarlos a desarrollar sus habilidades para resolver problemas y tener más confianza en su capacidad para factorizar trinomios. La tabla también puede ahorrar tiempo, ya que los estudiantes pueden evitar tener que adivinar y verificar diferentes combinaciones de factores.
La tabla proporciona una manera metódica para factorizar trinomios, que puede ser útil para los estudiantes que tienen dificultades con este tema.
2. Trinomios de la forma ax2 + bx + c
Aquí está cómo factorizar el trinomio 2x2 + 10x + 16 usando el método de convertirlo a la forma x2 + bx + c:
- Divida el trinomio por el coeficiente principal 2 para obtener:
- 2x2 + 10x + 16 = 2(x2 + 5x + 8)
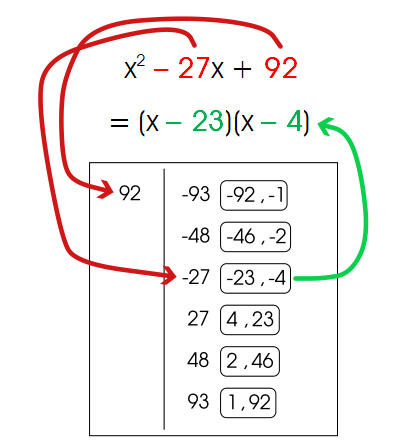
- Factoriza el trinomio x2 + 5x + 8 usando las técnicas de factorización apropiadas para esta forma. En este caso, podemos usar la tabla de factorización para encontrar que:
- x2 + 5x + 8 = (x + 4)(x + 1)
- Reescribe los factores en términos de las variables originales multiplicando cada factor por 2, para obtener:
- 2(x + 4)(x + 1) como la forma factorizada del trinomio original.
De esta manera, el trinomio 2x2 + 10x + 16 se puede factorizar como 2(x + 4)(x + 1) usando el método de convertirlo a la forma x2 + bx + c.
3. Para qué factorizar polinomios
Aprender a factorizar polinomios es una habilidad importante en matemáticas, y a los estudiantes se les enseña esta habilidad por varias razones, entre ellas:
- Simplificar expresiones: la factorización de polinomios puede ayudar a simplificar expresiones complejas al dividirlas en términos más simples. Esto puede facilitar la manipulación y resolución de ecuaciones.
- Resolver ecuaciones: factorizar polinomios es un paso clave para resolver muchos tipos de ecuaciones, incluidas ecuaciones cuadráticas y polinomios de mayor grado. Al factorizar un polinomio, los estudiantes pueden encontrar sus raíces, que son las soluciones de la ecuación.
- Representación gráfica de funciones: La factorización de polinomios puede ayudar a los estudiantes a representar gráficamente funciones más fácilmente. Al factorizar un polinomio, pueden identificar sus características clave, como sus intersecciones y puntos de inflexión, que se pueden usar para dibujar el gráfico.
- Comprensión de conceptos algebraicos: la factorización de polinomios puede ayudar a los estudiantes a desarrollar una comprensión más profunda de los conceptos algebraicos, como la propiedad distributiva, el máximo común divisor y la diferencia de cuadrados. Al factorizar polinomios, los estudiantes pueden ver cómo estos conceptos se aplican en la práctica.
La tabla puede ser utilizada por los estudiantes en lugar del tradicional método de prueba y error. Es una estrategia más sencilla que aplicar la ecuación cuadrática y puede ayudar a los estudiantes a realizar o verificar sus tareas de factoreo.
Otra manera de factorizar trinomios completos e incompletos es utilizar el método de Po-Shen Loh para lo cual también preparamos unos ejercicios de repaso.