Tabla de Raíces Cuadradas hasta el 1000 PDF gratis

Utiliza la clave neoparaiso.com para abrir el PDF.

Los números son los componentes básicos del universo matemático y comprender sus propiedades fundamentales es crucial para una variedad de aplicaciones. Uno de esos conceptos fundamentales que a menudo capta nuestra curiosidad matemática es la raíz cuadrada.

La raíz cuadrada perfecta:

En esencia, la raíz cuadrada perfecta de un número es el valor que, cuando se eleva al cuadrado, reproduce con precisión el número original. Por ejemplo, 3 es la raíz cuadrada perfecta de 9 porque 3 al cuadrado (3²) es igual a 9. De manera similar, 5 es la raíz cuadrada exacta de 25 porque 5 al cuadrado (5²) es igual a 25. Este concepto forma la base de muchos principios matemáticos y encuentra aplicaciones en diversos campos.

Raíces históricas:

El símbolo que utilizamos para representar raíces cuadradas tiene un origen interesante. El mérito de su introducción es del matemático alemán Christoff Rudolff, quien utilizó por primera vez el símbolo como una corrupción de la palabra latina "radix", que significa raíz. En 1525, hace casi cinco siglos, Rudolff introdujo este símbolo para indicar la raíz cúbica repitiéndolo tres veces. Esta visión histórica añade profundidad a nuestra comprensión de los símbolos y notaciones que encontramos en el discurso matemático.

Más allá de los números enteros:

Si bien nuestros encuentros iniciales con las raíces cuadradas a menudo involucran números enteros, es importante reconocer que este concepto se extiende más allá de los números enteros. La raíz cuadrada de un número también puede ser un decimal o una fracción. Por ejemplo, la raíz cuadrada de 10 es aproximadamente 3,16227. Puedes verificar esto multiplicando 3,16227 por sí mismo en una calculadora, lo que da como resultado un valor muy cercano a 10. En tales casos, nos referimos al número como un cuadrado imperfecto, y su raíz cuadrada tendrá un componente no entero, lo que nos presenta al fascinante reino de los decimales y las fracciones en las operaciones matemáticas.

Cuadrados imperfectos y precisión decimal:

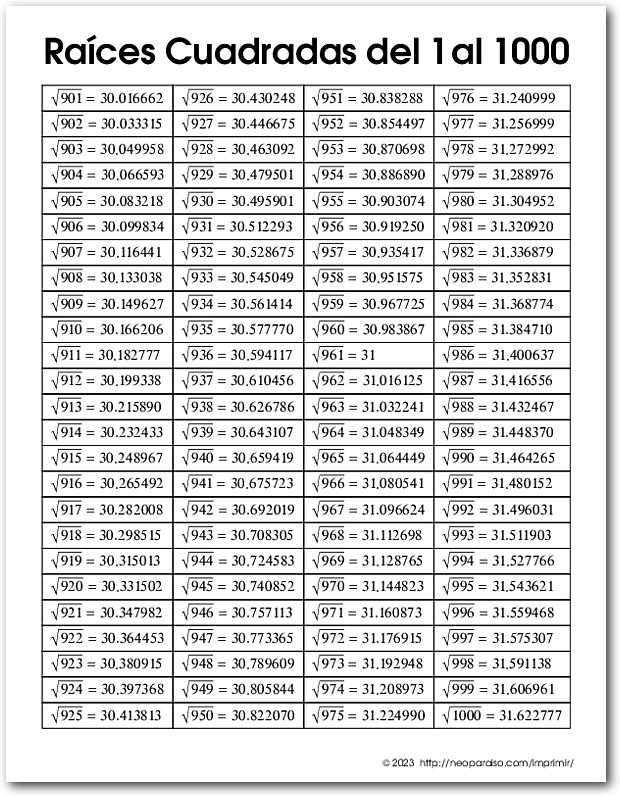
Para facilitar una exploración más profunda de las raíces cuadradas, la tabla adjunta proporciona valores para las raíces cuadradas de números que van del 1 al 1000. Este cuadro ofrece información sobre las raíces de cuadrados imperfectos, con valores redondeados a seis decimales de precisión. Comprender y calcular raíces cuadradas con tanta precisión permite realizar cálculos matemáticos más precisos, un aspecto crucial en campos como la física, la ingeniería y la informática.

La importancia práctica de las raíces cuadradas:

¿Por qué esto importa? La capacidad de encontrar raíces cuadradas es una habilidad fundamental con aplicaciones generalizadas. En campos como la física, donde es esencial comprender distancias, velocidades y fuerzas, las raíces cuadradas desempeñan un papel crucial. En ingeniería, al diseñar estructuras o circuitos, son necesarios cálculos precisos que involucran raíces cuadradas. Además, en informática, los algoritmos suelen basarse en raíces cuadradas para la optimización y la resolución de problemas.

Conclusión:

Al desentrañar los misterios de las raíces cuadradas, no sólo obtenemos una apreciación más profunda de la elegancia de los conceptos matemáticos sino que también reconocemos su importancia práctica en diversas disciplinas. Desde las raíces históricas del símbolo hasta la precisión de los cálculos decimales, el viaje al mundo de las raíces cuadradas revela un rico tapiz de belleza matemática que continúa dando forma a nuestra comprensión del universo numérico. Entonces, la próxima vez que encuentres una raíz cuadrada, recuerda los siglos de exploración matemática que nos han llevado a este momento de comprensión y apreciación.

LO MÁS DESCARGADO

Otros también vieron:

Tabla

Matemáticas

Síguenos en Facebook