Tabla de Catetos e Hipotenusas Notables PDF
Utiliza la clave neoparaiso.com para abrir el PDF.
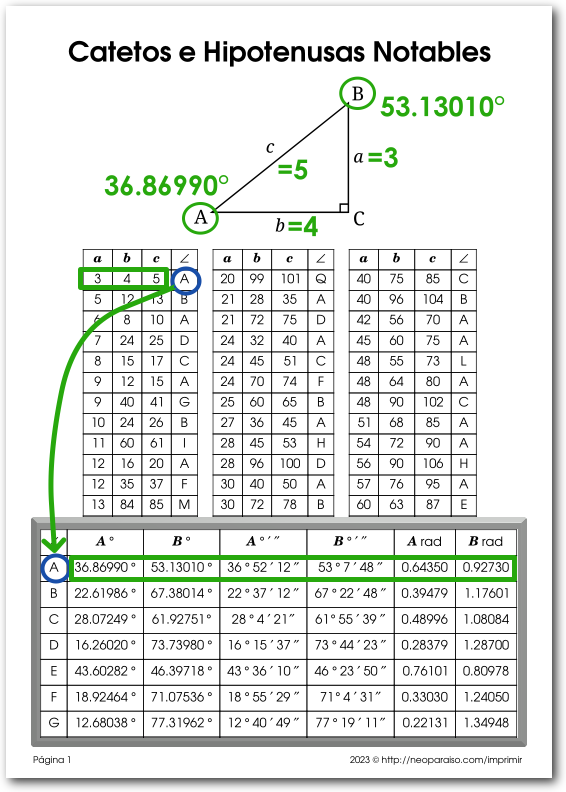
Una tabla de catetos e hipotenusas notables puede ser un recurso útil para los estudiantes que están aprendiendo sobre triángulos rectángulos y el teorema de Pitágoras. Las ternas de Pitágoras son conjuntos de tres números enteros positivos (a, b y c) que satisfacen el teorema de Pitágoras, que establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (c) es igual a la suma de los cuadrados de los otros dos lados (a y b): a 2 + b 2 = c 2
Así es como los estudiantes pueden usar esta tabla de catetos e hipotenusas:
- Verificación de triángulos con ángulo recto: dados tres números enteros positivos (a, b, c), los estudiantes pueden verificar si forman un triplete pitagórico. Pueden hacer esto buscando los números en la tabla si son números menores a 100, o reemplazando los valores en la ecuación del teorema de Pitágoras. Si es cierto (a2 + b2 = c^2), entonces los números forman un triángulo rectángulo.
- Generación de triángulos en ángulo recto: los estudiantes pueden usar la tabla para encontrar ternas pitagóricas y generar triángulos rectángulos con longitudes de lado enteras. Pueden elegir dos números cualesquiera (a y b) de la tabla y calcular el tercero (c) usando la tabla. Este proceso les ayuda a explorar varios triángulos rectángulos con lados enteros.
- Resolución de problemas de geometría: cuando se encuentren con problemas de geometría que involucren triángulos rectángulos, los estudiantes pueden usar la tabla para identificar ternas pitagóricas que se ajusten a las condiciones del problema. Esto puede simplificar los cálculos y hacer que la resolución de problemas sea más manejable.
- Comprensión de patrones: Observar la tabla puede ayudar a los estudiantes a notar patrones y relaciones entre los números en las ternas pitagóricas. Por ejemplo, podrían reconocer que algunas ternas son múltiplos de ternas más pequeñas o que ciertos conjuntos de ternas tienen un factor común.
- Aplicaciones de la vida real: Los estudiantes pueden usar la tabla para resolver problemas del mundo real que involucran triángulos rectángulos. Por ejemplo, en construcción o ingeniería, podrían usar las ternas para determinar longitudes o dimensiones.
- Explorando números irracionales: Al usar la tabla
, los estudiantes también pueden darse cuenta de que no todos los triángulos rectángulos tienen longitudes enteras de lados. El teorema de Pitágoras también se puede usar para demostrar la existencia de números irracionales, ya que algunos triángulos rectángulos tienen lados con longitudes irracionales.
Vale la pena señalar que, si bien la tabla puede ser útil para la exploración y la resolución de problemas, memorizar catetos e hipotenusas no debe ser el objetivo principal de aprender sobre el teorema de Pitágoras. Comprender el concepto y cómo aplicarlo es más importante. No obstante, tener a mano una tabla de ternas pitagóricas ciertamente puede ser beneficioso como referencia y herramienta para mejorar la comprensión.