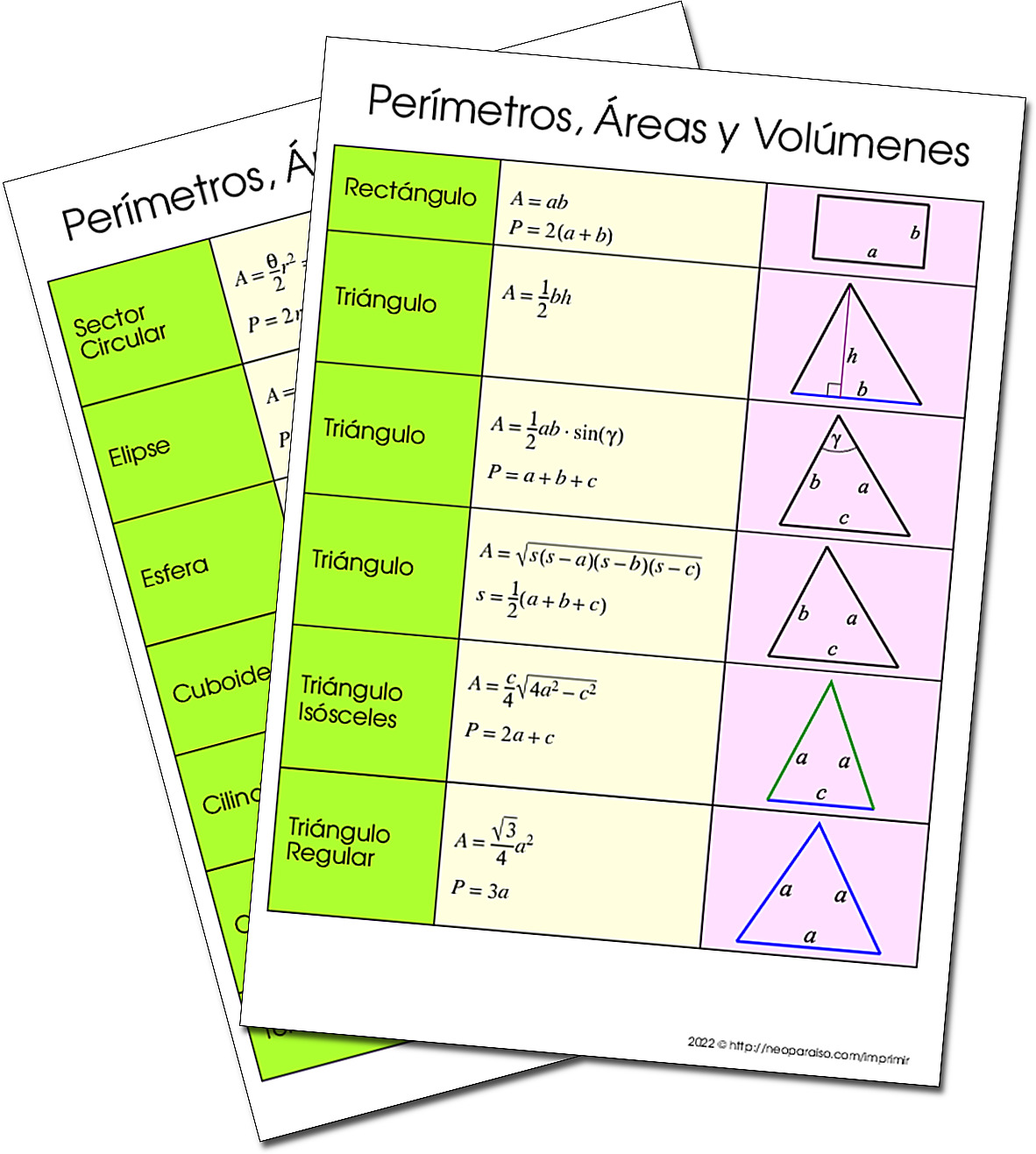
Fórmulas de Perímetro, Área y Volumen de Figuras Geométricas

Utiliza la clave neoparaiso.com para abrir el PDF.

Aprendizaje Esperado. Calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros, desarrollando y aplicando fórmulas.

En esta página vamos a aprender sobre varias fórmulas para el área, el perímetro y el volumen de varias formas y figuras geométricas. Para su conocimiento, un perímetro es el camino que rodea o abarca una forma bidimensional, más específicamente la longitud de ese camino. Un perímetro significa la distancia del límite de una forma bidimensional. Además, se define como la suma de la longitud de todos los lados del objeto. La suma de la longitud de cada lado es el perímetro de esa forma.

Mientras que el volumen es la cantidad de un espacio tridimensional encerrado por una superficie cerrada. Cuando llenas un frasco con canicas o llenas una piscina con agua, ¡estás determinando volumen!

Y el área es la cantidad de espacio plano que ocupa una figura o forma bidimensional. El área de una forma se puede determinar colocando la forma sobre una cuadrícula y contando el número de cuadrados que cubren todo el espacio. Existen otras maneras.

En geometría, hay diferentes formas y figuras, como esfera, cubo, paralelepípedo, cono, cilindro, etc. Cada forma tiene su área de superficie y su volumen. Pero en el caso de figuras bidimensionales como cuadrado, círculo, rectángulo, triángulo, podemos medir solo el área cubierta por estas figuras ya que no tienen volumen. Por ejemplo, no se puede encontrar el volumen del círculo, aunque sí se puede encontrar el volumen de la esfera. Es así porque una esfera es una figura tridimensional.

• La geometría es una rama de las matemáticas que se ocupa de diferentes formas y tamaños. Se puede dividir en dos tipos diferentes: Geometría Plana y Geometría Sólida
• La geometría plana se ocupa de formas como círculos, triángulos, rectángulos, cuadrados.
• La geometría de cuerpos sólidos se ocupa de cuerpos en el espacio: cubos, esferas, prismas, pirámides, sólidos platónicos, cilindros, conos.
• La medición es una rama de las matemáticas que se ocupa del área, el perímetro, y el volumen de varias formas geométricas. Es uno de los capítulos más importantes cubiertos en Matemáticas de 6to grado y secundaria. La medición tiene inmensas aplicaciones prácticas en nuestro día a día. Las fórmulas de área tienen muchas aplicaciones prácticas en la construcción, la agricultura, la arquitectura y la ciencia.

El perímetro se mide en unidades lineales, el área se mide en unidades cuadradas y el volumen se mide en unidades cúbicas.

Un área de estudio importante para todo estudiante de la materia de matemáticas son las fórmulas de geometría. Se utilizan para calcular la longitud, el perímetro, el área y el volumen de varias formas y figuras geométricas. Hay muchas fórmulas geométricas, que están relacionadas con la altura, el ancho, la longitud, el radio, el perímetro, el área, la superficie o el volumen y mucho más.

En 5to grado se iniciará el estudio del perímetro, al calcular su medida en diversas figuras como polígonos regulares e irregulares y figuras curvilíneas incluyendo círculos. Explique a los alumnos que pueden determinar el perímetro de varias maneras: sumando las medidas de todos los lados; transportando un lado tras otro sobre una regla graduada; tomando un hilo, colocándolo sobre el contorno de una figura y haciendo una marca en el hilo una vez que se ha haya rodeado esta última, después se estira el hilo y se mide hasta la marca con una regla graduada.

El último procedimiento es particularmente útil cuando las figuras tienen lados curvos. Se puede analizar la relación entre el perímetro y el diámetro de varios círculos e identificar que la razón entre ambas es constante y es un número al que se denomina pi, el cual se representa con la letra griega p. Es importante que sean los alumnos quienes, a partir de actividades, encuentren el factor de proporcionalidad (p) que hay entre la medida de la circunferencia y el diámetro.

Los alumnos de 6to grado continuarán el estudio de las superficies al calcular el área de triángulos y cuadriláteros (rombos, romboides y trapecios) mediante su transformación en un rectángulo. Es importante mencionar que no es propósito de este grado construir las fórmulas usando expresiones algebraicas, esto se reserva para el primer grado de secundaria, pero sí que se expresen verbalmente, por ejemplo:

Otro tipo de actividades recomendables son las que apuntan a diferenciar el perímetro y el área de una figura y a descubrir que no necesariamente a mayor perímetro corresponde mayor área.

Así los alumnos de 6to grado empezarán a estudiar una nueva magnitud: el volumen. Es importante comparar objetos claramente distintos unos de otros por su forma o el material de que estén hechos (excepto los que son porosos, como la piedra pómez, o con perforaciones o huecos), y que los alumnos comparen su volumen sumergiéndolos en agua: el cuerpo que desplace más agua es el de mayor volumen.

Algunas fórmulas geométricas son bastante complicadas y es posible que casi nunca las veas, sin embargo, hay algunas fórmulas básicas que se utilizan en nuestra vida diaria para calcular la longitud, el área y el volumen.

Aquí hay algunas fórmulas básicas que se pueden usar para calcular la longitud, el área, el volumen y el perímetro de varias formas y figuras.

Es necesario descargar e imprimir el formulario . Puede descargarlo el archivo a su computadora e imprimir las hojas de forma gratuita para cada uno de sus alumnos. Utilize la clave neoparaiso.com para abrirlo. Pero tenga en cuenta que cualquier redistribución de este material no está permitida.

LO MÁS DESCARGADO

Otros también vieron:

Fórmulas

Figuras Geométricas

Matemáticas

Síguenos en Facebook