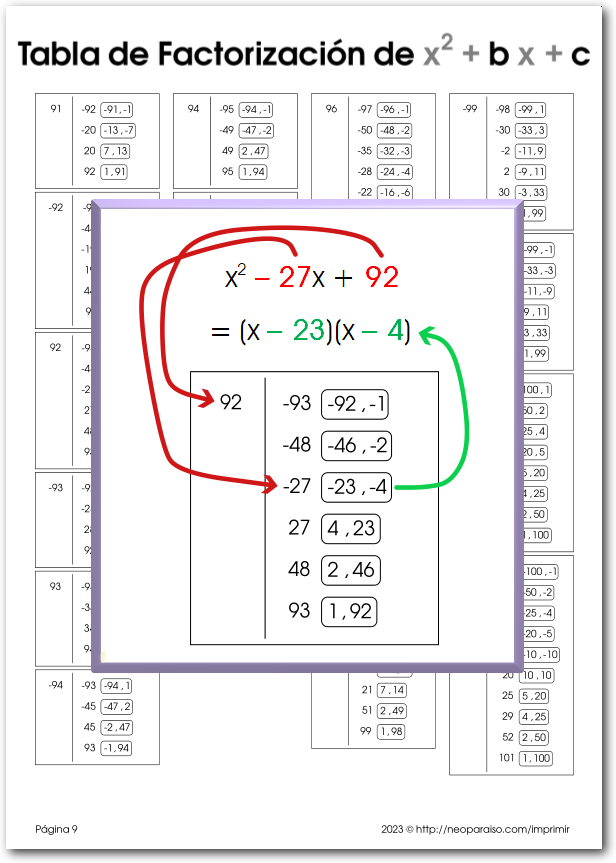
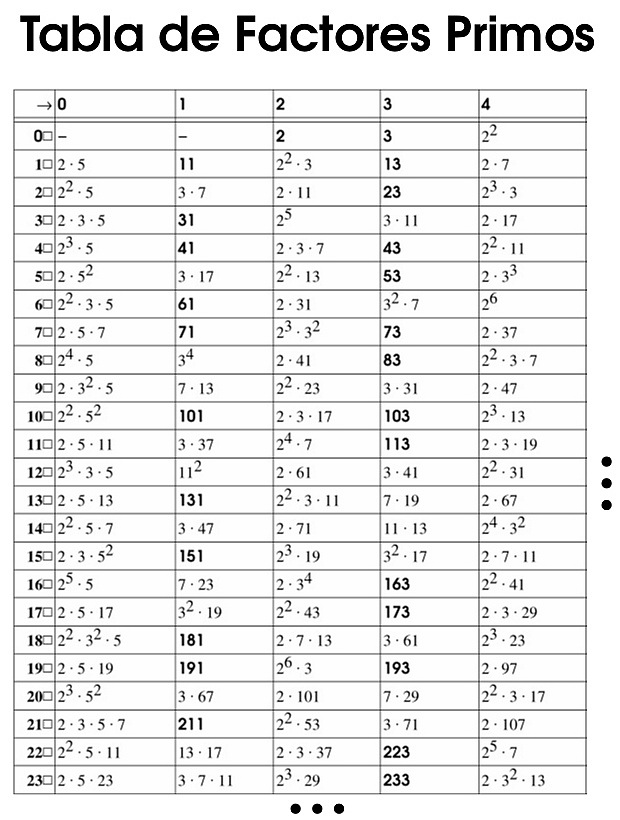
Tabla de Números Primos para Imprimir
Utiliza la clave neoparaiso.com para abrir el PDF.
1. Factores Primos que son?
Encontrar los factores primos de un número dado. En teoría de números, los factores primos de un entero positivo son los números primos que dividen ese entero exactamente. Así por ejemplo, 2 es factor primo del número 100 porque 100/2 = 50 exactamente. La descomposición en factores primos de un entero positivo es una lista de los factores primos del entero, junto con sus multiplicidades; el proceso de determinación de estos factores se llama factorización de enteros o descomposición canónica.
Factorizamos números en matemáticas por una variedad de razones. Una de las principales razones para factorizar un número es determinar si es primo o compuesto. Un número primo es un número entero que tiene solo dos divisores enteros: 1 y él mismo. Un número compuesto es un número entero que tiene más de dos divisores enteros. Al factorizar un número, podemos determinar cuántos divisores enteros tiene y si es primo o compuesto.
Otra razón para factorizar números es realizar operaciones aritméticas, como suma, resta, multiplicación y división. Por ejemplo, si queremos dividir un número por otro, primero podemos factorizar ambos números y luego cancelar cualquier factor común para simplificar la operación. La factorización de números también puede ser útil para resolver ecuaciones y otros problemas matemáticos.
Hay muchas otras razones para factorizar números en matemáticas, y la razón específica para hacerlo dependerá de la situación y los objetivos de la persona que realiza la factorización.
Aquí hay algunas otras razones para factorizar números en matemáticas:
- Simplificar expresiones y ecuaciones algebraicas cancelando factores comunes.
- Para encontrar el máximo común divisor de dos o más números.
- Expresar un número como producto de sus factores primos, lo que puede ser útil para resolver ciertos problemas matemáticos.
- Para encontrar el mínimo común múltiplo de dos o más números.
- Resolver problemas de fracciones expresando el numerador y el denominador como producto de factores primos.
- Encontrar las raíces de ecuaciones polinómicas usando la factorización del polinomio.
Estas son solo algunas de las muchas razones para factorizar números en matemáticas. La factorización es una habilidad útil que se utiliza en muchas operaciones y aplicaciones matemáticas diferentes.
2. Cómo hacer una tabla de números primos?
Descripción detallada del proceso de construcción de una criba de Eratóstenes hasta el 200.
A nivel escolar, una comprensión sólida de los números primos y los factores tiene muchos usos, porque todos los números están formados por números primos.
Si un número se expresa como el producto de sus factores primos, entonces:
- En primer lugar
Todas las propiedades de ese número se pueden ver de un vistazo.
Por ejemplo, se puede saber si es impar o par? primo, compuesto?, un cuadrado, un cubo o cualquier otra potencia?
- En segundo lugar
Todos los divisores de un número pueden determinarse utilizando diferentes combinaciones de los factores primos.
- En tercer lugar
Una vez que se conoce el producto de los factores primos, es fácil calcular la raíz cuadrada, la raíz cúbica o cualquier otra raíz.
- Cuarto lugar
Es posible determinar cómo se puede convertir el número en un cuadrado o cubo, etc., multiplicando por factores faltantes.
- En quinto lugar
Usar factores primos es una manera fácil de encontrar el MCM o el MCD de números más grandes.
También en factorizar trinomios cuadráticos.
Lamentablemente, el uso de números primos se infrautiliza en la escuela secundaria, donde se les pide a los estudiantes que escriban un número como producto de sus factores primos, pero se hace poco uso de él.
Está es una Criba de Eratóstenes hasta el número 6499, para imprimir. La segunda fila corresponde a los números empezando el 100, así 101 es primo, 103 es primo, 107 es primo. La tercera fila corresponde a los números empezando en 200, así 211 es primo, 223 es primo, etc. Está contenida en una hoja formato A4, en PDF .