Tarjetas de Diagramas de Factores

Tarjetas de Diagramas de Factores. Tarjetas de Puntos de Números del 1 al 100. Puntos agrupados hasta el 100. Tarjetas de Factorización. Juegos para trabajar y repasar los números primos y la descomposición de factores primos. Juegos de Factorización. Juegos Matemáticos para imprimir.

Utiliza la clave neoparaiso.com para abrir el PDF.

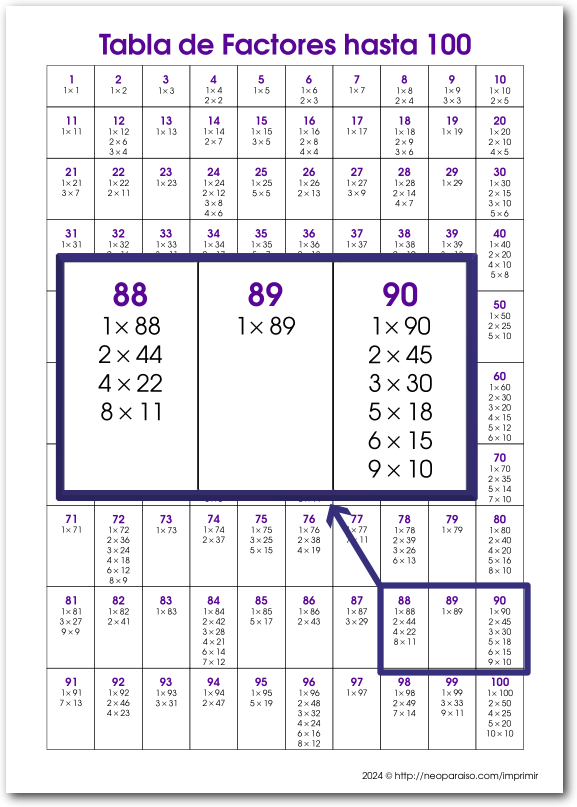
Explore los números primos y la factorización con esta hermosa baraja de cartas, adecuada para el aula o para uso personal. Cada tarjeta muestra un diagrama de factorización en un lado, que representa visualmente la descomposición en factores primos de un número entero, y el número mismo en el otro lado. La baraja contiene los números del 1 al 100. ¡Úselas como tarjetas didácticas, organícelas y busque patrones, o invente sus propias actividades y juegos! Aqui algunas propuestas de juegos con factores primos:

1. Juego de Multiplicación para Identificar el Número de Puntos

Poner una tarjeta en el centro del grupo. El primero en identificar el valor toma la tarjeta. Continuar hasta que se tomen todas las cartas. El jugador con más cartas es el ganador.

Una estrategia eficaz es repasar las tablas de multiplicar e identificar visualmente grupos idénticos, contarlos, y contar sus elementos. Luego multiplicar mentalmente para hallar el valor total de puntos sin contarlos individualmente uno a uno.

2. Juego Clásico de Guerra

Pueden jugar un juego similar al clásico de Guerra: Se reparten las cartas entre todos los jugadores, dos o tres jugadores. Todos muestran simultáneamente la carta superior de su mazo. Quien muestra la carta mayor captura todas y las aparta. Cuando los jugadores simultáneamente muetran la última carta de su mazo el juego acaba y el jugador que haya capturado más cartas gana.

La diferencia de esta versión es que mientras juegan solamente deben mirar el lado del diagrama de puntos de las cartas, no el lado con el número escrito. Entonces, parte del juego es averiguar qué diagrama de factorización representa un número mayor. Por supuesto, uno podría simplemente contar los puntos de cara tarjeta y luego compararlo, pero imagino que los estudiantes también pueden encontrar trucos que pueden usar para decidir cuál es más grande sin contar completamente cuántos puntos tiene cada una.

Puede escogerse un subconjunto interesante de las tarjetas, por ejemplo sacar del mazo las cartas que correspondend a números primos altos, o también eliminar cartas de números muy bajos y simples.

Variante 1: los primos son comodines, es decir, los primos siempre superan a los números compuestos. (Si tiene dos números primos o dos números compuestos, entonces el más alto vence al más bajo como de costumbre). Esto puede hacer que el juego sea un poco más fácil, ya que cuando se juega un número primo no es necesario contar su valor para compararlo con cualquier número compuesto jugado en oposición a él.

Variante 2: como la variante 1, excepto que los primos solo superan a los números compuestos que no los tienen como factor. Por ejemplo, 5 vence a 24, pero 5 pierde ante 30: dado que 30 tiene 5 como factor primo, es "inmune" a 5.

Como una actividad divertida de continuación de la variante 2, intente hacer una lista de las cartas en orden según cuál vence a cuál.

3. Juego SET

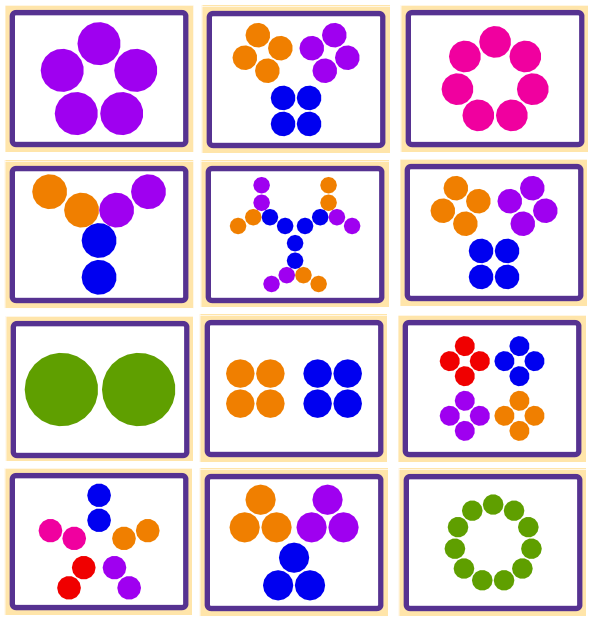
Una variante divertida de SET. Comience repartiendo doce tarjetas de factorización, con el diagrama hacia arriba. Al igual que el juego SET habitual, el objetivo es encontrar y reclamar conjuntos de tres cartas. La diferencia está en cómo se definen los conjuntos. Un “conjunto” de cartas de factorización es cualquier conjunto de tres cartas que:

No comparten factores primos en común (es decir, cualquier primo dado ocurre como máximo en una de las cartas), o
Comparten todos sus factores primos en común (cada primo que aparezca en cualquiera de las cartas debe aparecer en las tres).

Estos son algunos ejemplos de conjuntos válidos:

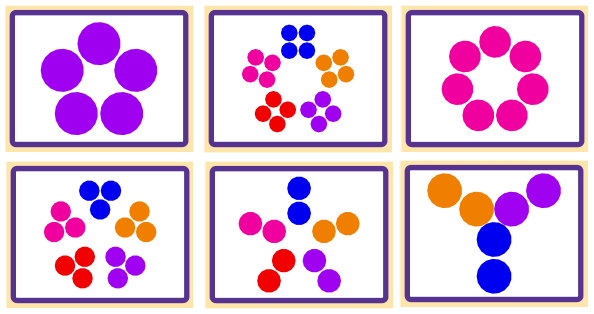
Y aquí hay algunos conjuntos no válidos:

Para reclamar un conjunto, deben indicar el número en cada tarjeta y explicar por qué forman un conjunto. Si están en lo correcto, retiren las cartas y repartan tres cartas nuevas. Si están equivocados, ¡siguen buscando!

El archivo contiene las tarjetas con los diagramas de factores. Está en formato PDF. Utiliza la clave neoparaiso.com para abrir el PDF.

4. Aplicación

Estos juegos pueden ser utilizados en una variedad de escenarios, para practicar la descomposición en factores primos:

Quién termina más rápido: Se pueden repartir tarjetas idénticas a parejas de estudiantes y hacer una competencia de velocidad, con premios, para los estudiantes que completen primero.

Actividad Extra: El juego es una actividad perfecta para aquellos niños que terminan su trabajo temprano y se quedan sin tener qué hacer. Se puede imprimir y conservar en una caja de juegos o en un estante donde los niños puedan acceder a ella cuando terminen su trabajo.

Estudiantes como Maestros: Una actividad que realmente vale la pena es que algunos niños aprendan el juego y luego enseñen a otros. Enseñar a otros cómo jugar es una gran actividad de comunicación.

Estudiantes como Maestros: Colocar varias de estas tarjetas ordenadas en una mesa para una actividad De qué te das cuenta, Qué te preguntas.

5. De qué te das cuenta, Qué piensas, Qué te preguntas

Esta propusta parte del concepto de Pensamiento Visible que consiste en crear condiciones para pensar como: la curiosidad, la comprensión y la creatividad. El aprendizaje es resultado del pensamiento. Esto nos lleva a concientizar la importancia de promover el pensamiento en los estudiantes y hacerlo visible para que el estudiante entienda su forma de aprender.

Nuestro pensamiento es por naturaleza invisible para las personas que están a nuestro alrededor. El Pensamiento Visible es una iniciativa, con el fin de poner al descubierto el pensamiento de

las personas. El lenguaje, tanto oral como escrito, es el medio más común para exteriorizar el pensamiento de las personas.

Es una propuesta abierta que hace que los estudiantes hablen sobre escenarios matemáticos de una manera cuidadosa y no amenazante. El recurso de esta página fue desarrollado para ayudar a las maestras a llevar esta práctica a su salón de clases.

Reparta o proyecte una lámina o cartel, imagen, descripción de una situación (sin preguntas), tabla de datos, etc. Pida a los estudiantes que consideren estas dos preguntas: ¿Qué notan? ¿Qué piensan? ¿Qué se preguntan?

5.1. Tiempo individual para pensar

Dé a los estudiantes algo de tiempo para que lo vean por su cuenta antes de hablar con los demás. Los estudiantes deben escribir al menos 2 cosas que noten y 2 cosas que se pregunten.

5.2. Lluvia de ideas sobre más en parejas

Si hay tiempo, pida a los estudiantes que hablen en parejas sobre lo que notan (lo que les llama la atención) y lo que se preguntan (qué preguntas tienen). Pídeles que tomen notas sobre las percepciones y dudas de los demás. Desafíelos a pensar en al menos una pregunta nueva que no hayan tenido antes.

5.3. Compartir en grupo

Reúna a los estudiantes para una conversación de grupo general. Tome notas en dos columnas. Podrías decir: “Tú eres el cerebro y yo soy la mano. Dile a mi mano qué escribir.” Toma notas sin evaluar.

5.4. Discutir, "¿Qué notan?"

Haga una pausa para permitir que la mayor cantidad posible de estudiantes levanten la mano. Llame a los estudiantes y registre sus observaciones al frente del salón.

A medida que registra los pensamientos de los estudiantes, agradezca o reconozca a cada estudiante por igual. Registre todas las sugerencias de los estudiantes. Evite corregir, elogiar, reafirmar, aclarar o hacer preguntas. Evite evaluar declaraciones. Ellos son el cerebro, usted eres la mano.

5.5. Pregunte a los estudiantes, "¿Qué se preguntan?"

Haga una pausa para permitir que la mayor cantidad posible de estudiantes levanten la mano. Llame a los estudiantes y registre sus dudas al frente del salón. Escriba las preguntas sin responderlas.

Pregunte a los estudiantes: “¿Hay algo aquí arriba que se estén preguntando? ¿Algo que necesiten aclarar? ¿Tiene alguna pregunta sobre algo que alguien notó o preguntó?” Si usted o los estudiantes tienen preguntas sobre algún elemento, pídales a los estudiantes que las compartieron que las aclaren más.

5.6. Pensamiento Visible

El Pensamiento Visible promueve el desarrollo de funciones ejecutivas que permiten al niño conocerse a sí mismo, y por ende autorregularse; así el niño aprende a aprender. El niño, cuando conoce su forma de pensar y resolver problemas, está más apto para: hacer conexiones con experiencias previas, manejar sus emociones y autocorregirse.