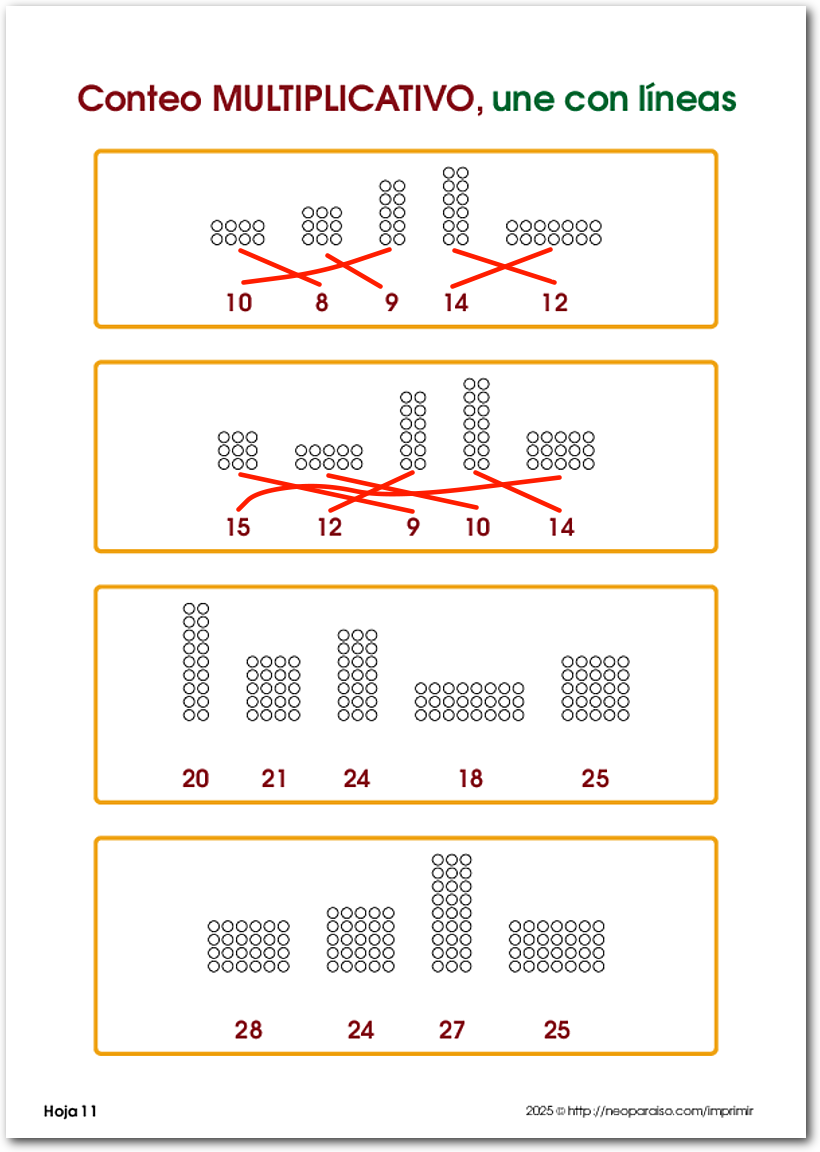
Lámina de Conteo de Multiplicativo

Lámina de Conteo de Multiplicativo. La cuadrícula de multiplicación de escala real. Arreglos Rectangulares. Tabla Pitagórica. La Tabla de Multiplicar con puntos a Color para los niños con Inteligencia Visual. Tabla de Multiplicar a Colores. Cuadro Multiplicativo de Puntos para Contar.

Utiliza la clave neoparaiso.com para abrir el PDF.

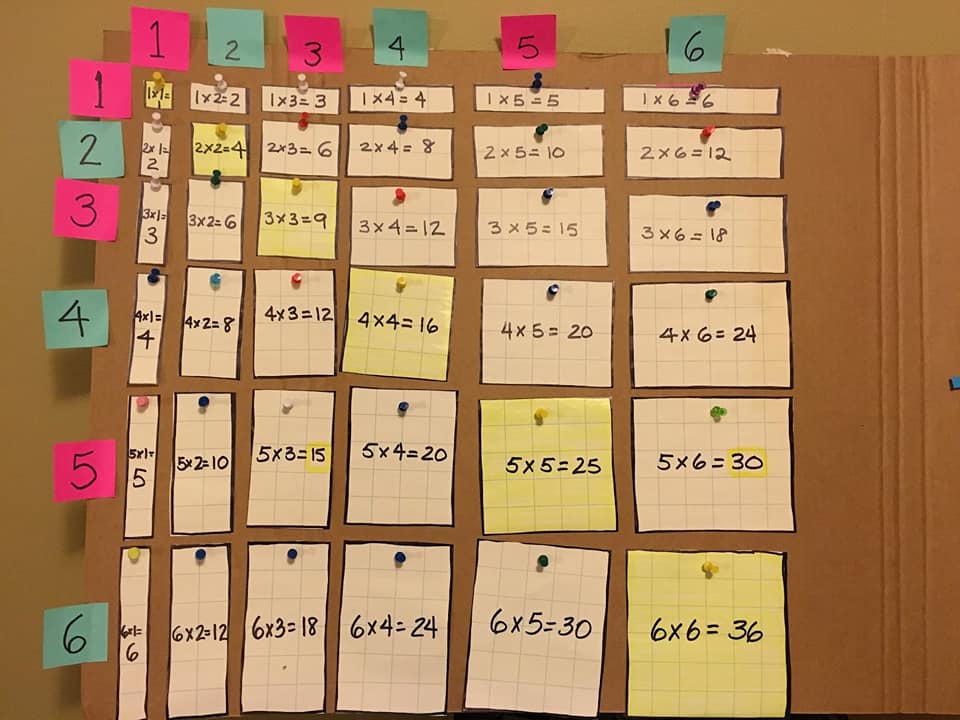
Este documento contiene la tabla de Pitágoras que tu niño puede usar como ayuda para memorizar las tablas. Está en formato PDF por lo que es fácilmente imprimible. La discusión y exploración de estas relaciones entre los valores de la grilla ayudarán a afianzar la memorización.

Como definición diremos que la tabla pitagórica es una matriz de números, se caracteriza porque el valor de la columna j-ésima de la fila i-ésima es el producto de i a j.

Una buena idea para una cuadrícula de multiplicación con énfasis en lo visual ha estado dando vueltas en la Internet recientemente:

Me encantó leer comentarios y ver cómo la gente ya está usando las cuadrículas, con otros maestros, estudiantes y sus propios hijos. A algunos de ustedes se les ocurrieron ideas para variaciones que podría hacer, incluido comenzar la cuadrícula desde la parte inferior izquierda para imitar una cuadrícula de coordenadas cartesianas y enfatizar los números de la diagonal (los cuadrados). He reunido varias de las ideas en un solo documento pdf para facilitar el acceso.

Mi plan con estas tablas de multiplicar era facilitar a los alumnos una intuición más clara para la multiplicación. Creo firmemente que la mayoría de las dificultades que encuentran los estudiantes con temas "difíciles" como proporciones, fracciones y álgebra generalmente se derivan de una comprensión y familiaridad inadecuadas de la multiplicación. No tiene sentido tratar de enseñar paréntesis anidados hasta que la propiedad distributiva tenga sentido numéricamente, por ejemplo, y un tipo de instrumento visual correcto podría ayudar a los estudiantes a ver no solo el qué es lo que resulta de una multiplicación, sino también el por qué se obtienen los resultados que se obtienen al multiplicar.

Se puede utilizar para realizar a mano cualquier multiplicación con el sistema de numeración decimal. En el campo de la educación, cada fila y / o columna de dicha tabla se llama "tabla de multiplicar": por ejemplo, la cuarta fila (o columna) se llama la "tabla del cuatro".

La ley conmutativa de los números se aprecia en la tabla de multiplicar y de esta se derivan numerosas y curiosas propiedades y relaciones o regularidades. Por ejemplo, los valores de la diagonal que va de la esquina superior izquierda a la esquina inferior derecha son todos los números al cuadrado, 1, 4, 9, 16, Se puede ver que efectivamente es un cuadrado la figuras que forman los puntos en esta diagonal. También, por encima y a la derecha de la diagonal, todos los números son el reflejo de los números por debajo y a la izquierda de la diagonal, es decir los valores contrarios son los mismos. Por ejemplo, al contar el resultado de 1x2 resulta igual que el opuesto 2x1. Tienen la misma cantidad de puntos, aunque los rectángulos estén rotados 90 grados.

Pueden verse varias representaciones visuales de números por ejemplo:

6 = 1 x 6 = 2 x 3 = 3 x 2 = 6 x 1
8 = 1 x 8 = 2 x 4 = 4 x 2 = 8 x 1
10 = 1 x 10 = 2 x 5 = 5 x 2 = 10 x 1
12 = 2 x 6 = 3 x 4 = 4 x 3 = 6 x 2
40 = 4 x 10 = 5 x 8 = 8 x 5 = 10 x 4

Así, ocho objetos pueden ser ordenados de manera rectangular de 4 diferentes maneras, 1 fila de 8 columnas, 2 filas de 4 columnas, 4 filas de 2 columnas, o 8 filas de 1 columna. Son 4 arreglos rectangulares.

El póster es una excelente decoración a cualquier salón de clases de primaria. El cartel muestra los productos del 1 al 9 como matrices o cuadrículas de puntos también conocidos como arreglos rectangulares. Un gran póster para una actividad De qué te das cuenta, Qué te preguntas.

1. Descripción de la Actividad

Qué te das cuenta, Qué te preguntas es una propuesta abierta que hace que los estudiantes hablen sobre escenarios matemáticos de una manera cuidadosa y no amenazante. El recurso de esta página fue desarrollado para ayudar a las maestras a llevar esta práctica a su salón de clases.

Reparta o proyecte una lámina o cartel, imagen, descripción de una situación (sin preguntas), tabla de datos, etc. Pida a los estudiantes que consideren estas dos preguntas: ¿Qué notan? ¿Qué se preguntan?

1.1. Tiempo individual para pensar

Dé a los estudiantes algo de tiempo para que lo vean por su cuenta antes de hablar con los demás. Los estudiantes deben escribir al menos 2 cosas que noten y 2 cosas que se pregunten.

1.2. Lluvia de ideas sobre más en parejas

Si hay tiempo, pida a los estudiantes que hablen en parejas sobre lo que notan (lo que les llama la atención) y lo que se preguntan (qué preguntas tienen). Pídeles que tomen notas sobre las percepciones y dudas de los demás. Desafíelos a pensar en al menos una pregunta nueva que no hayan tenido antes.

1.3. Compartir en grupo

Reúna a los estudiantes para una conversación de grupo general. Tome notas en dos columnas. Podrías decir: “Tú eres el cerebro y yo soy la mano. Dile a mi mano qué escribir.” Toma notas sin evaluar.

1.4. Discutir, "¿Qué notan?"

Haga una pausa para permitir que la mayor cantidad posible de estudiantes levanten la mano. Llame a los estudiantes y registre sus observaciones al frente del salón.

A medida que registra los pensamientos de los estudiantes, agradezca o reconozca a cada estudiante por igual. Registre todas las sugerencias de los estudiantes. Evite corregir, elogiar, reafirmar, aclarar o hacer preguntas. Evite evaluar declaraciones. Ellos son el cerebro, usted eres la mano.

1.5. Pregunte a los estudiantes, "¿Qué se preguntan?"

Haga una pausa para permitir que la mayor cantidad posible de estudiantes levanten la mano. Llame a los estudiantes y registre sus dudas al frente del salón. Escriba las preguntas sin responderlas.

Pregunte a los estudiantes: “¿Hay algo aquí arriba que se estén preguntando? ¿Algo que necesiten aclarar? ¿Tiene alguna pregunta sobre algo que alguien notó o preguntó?” Si usted o los estudiantes tienen preguntas sobre algún elemento, pídales a los estudiantes que las compartieron que las aclaren más.

2. Multiplicación como Área

Matemáticas básicas para enfatizar

El área de un rectángulo se puede medir llenándolo de unidades cuadradas en mosaico.
La longitud de una dimensión de un rectángulo indica cuántos cuadrados unitarios hay en cada fila de una cuadrícula que cubre el rectángulo.
La longitud de la otra dimensión del rectángulo indica cuántos cuadrados unitarios hay en cada columna de esa cuadrícula.
El área de los rectángulos se puede determinar multiplicando la longitud de los dos lados. Ese producto nos dice cuántos cuadrados unitarios cubren el rectángulo.

Una secuencia posible es comenzar con un trabajo en el que un estudiante cuente unidades (puntos) una por una, luego pasar a una en la que el alumno agrupe los puntos por filas o columnas, luego comparta una en la que el alumno multiplicó las longitudes de los lados.