Conversor de Bases
Utiliza la clave neoparaiso.com para abrir el PDF.
Necesitamos convertir entre bases numéricas cuando queremos representar números usando un sistema numérico diferente. Por ejemplo, usamos el sistema numérico decimal (base 10) en la vida cotidiana, pero las computadoras usan el sistema numérico binario (base 2) para representar números. Para comunicarnos con las computadoras, necesitamos poder convertir números del sistema decimal al sistema binario y viceversa. De manera similar, es posible que necesitemos convertir entre bases numéricas para realizar operaciones matemáticas o para representar números grandes en una forma más compacta. Hay muchas otras situaciones en las que la conversión entre bases numéricas puede ser útil o necesaria.
Los números hexadecimales (base 16) se utilizan en muchos campos diferentes, incluidas las ciencias de la computación, las matemáticas y la ingeniería. En el campo de la informática, los números hexadecimales se usan comúnmente para representar colores en una pantalla de computadora, así como para representar datos en una forma compacta y eficiente. En matemáticas, los números hexadecimales a menudo se usan para representar números muy grandes que son difíciles de representar usando el sistema numérico decimal (base 10). En ingeniería, los números hexadecimales a veces se usan para representar valores numéricos asociados con colores específicos, como los colores de un semáforo o los colores de un arco iris. Hay muchos otros usos para los números hexadecimales en diferentes campos.
Las propiedades de los números octales (base 8) son similares a las propiedades de otros sistemas numéricos. Algunas de las propiedades clave de los números octales incluyen:
- Los números octales usan los dígitos del 0 al 7 para representar números.
- Cada dígito en un número octal representa una potencia de 8. Por ejemplo, en el número octal 356, el dígito 5 representa 5 x 81 y el dígito 6 representa 6 x 80.
- Los números octales se pueden convertir hacia y desde otros sistemas numéricos, como decimal y binario, mediante operaciones matemáticas.
- Los números octales se pueden usar para realizar operaciones aritméticas, como suma, resta, multiplicación y división.
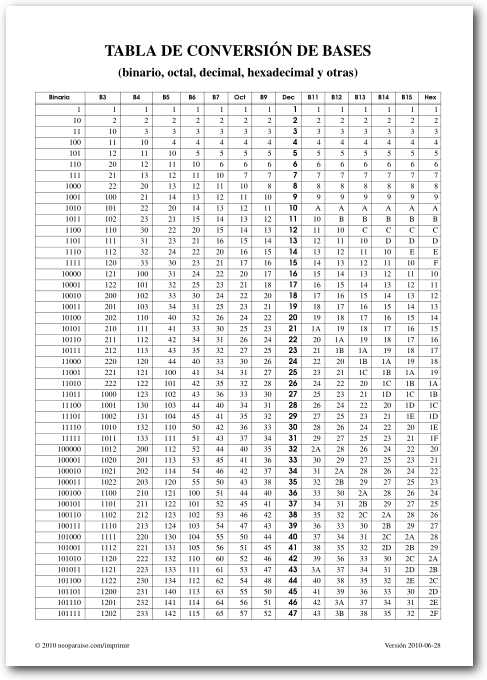
Para saber cómo hacer la conversión del sistema númerico base 10 (decimal) a otras bases, puedes ubicar tu número en la columna de la base 10 y luego buscar su equivalente en las otras columnas. De igual manera puedes convertir de binario a octal, de binario a hexadecimal, y todas las combinaciones posibles entre los diferentes sistemas numéricos. El cambio de base se realiza instantáneamente.
Binario es base 2, Octal es base 8, Decimal es base 10, Hexadecimal es base 16.
También puede servir para ver la propiedades de los números en diferentes bases: cómo van cambiando de acuerdo al sistema posicional de cada uno, cómo van siguiéndose los dígitos disponibles, cómo podrían existir más dígitos que los usuales del 0 al 9 utilizando las letras del alfabeto, o símbolos arbitrarios.
El método utilizado para general la tabla consiste en convertir números decimales a cada una de las bases con el procedimiento siguiente:
Conversión del número 234 a base 2
234 dividido entre 2 da 117 y el resto es igual a 0
117 dividido entre 2 da 58 y el resto es igual a 1
58 dividido entre 2 da 29 y el resto es igual a 0
29 dividido entre 2 da 14 y el resto es igual a 1
14 dividido entre 2 da 7 y el resto es igual a 0
7 dividido entre 2 da 3 y el resto es igual a 1
3 dividido entre 2 da 1 y el resto es igual a 1
1 dividido entre 2 da 0 y el resto es igual a 1
Ordenamos los restos, del último al primero: 11101010
Conversión del número 234 a base 8
234 dividido entre 8 da 29 y el resto es igual a 2
29 dividido entre 8 da 3 y el resto es igual a 5
3 dividido entre 8 da 0 y el resto es igual a 3
Ordenamos los restos, del último al primero: 352
Conversión del número 234 a base 16
234 dividido entre 16 da 14 y el resto es igual a 10
(El siguiente dígito luego del 9 es A)
14 dividido entre 16 da 0 y el resto es igual a 14
(El décimo cuarto dígito es E)
Ordenamos los restos, del último al primero: EA
Conversión del número 234 a base 5
234 dividido entre 5 da 46 y el resto es igual a 4
46 dividido entre 5 da 9 y el resto es igual a 1
9 dividido entre 5 da 1 y el resto es igual a 4
1 dividido entre 5 da 0 y el resto es igual a 1
Ordenamos los restos, del último al primero: 1414
El archivo en PDF tiene 22 páginas para imprimir en hojas de formato A4. En total las tablas contienen todos los números binarios hasta el 1000, los números octales hasta el 1000, los números hexadecimales hasta el 1000, etc. Utilice la contraseña neoparaiso.com para abrirlo. Puede descargarlo para su computadora e imprimirlo de forma gratuita, pero no redestribuirlo, o subirlo a redes sociales.