Hojas de Conteo de Multiplicativo
Utiliza la clave neoparaiso.com para abrir el PDF.
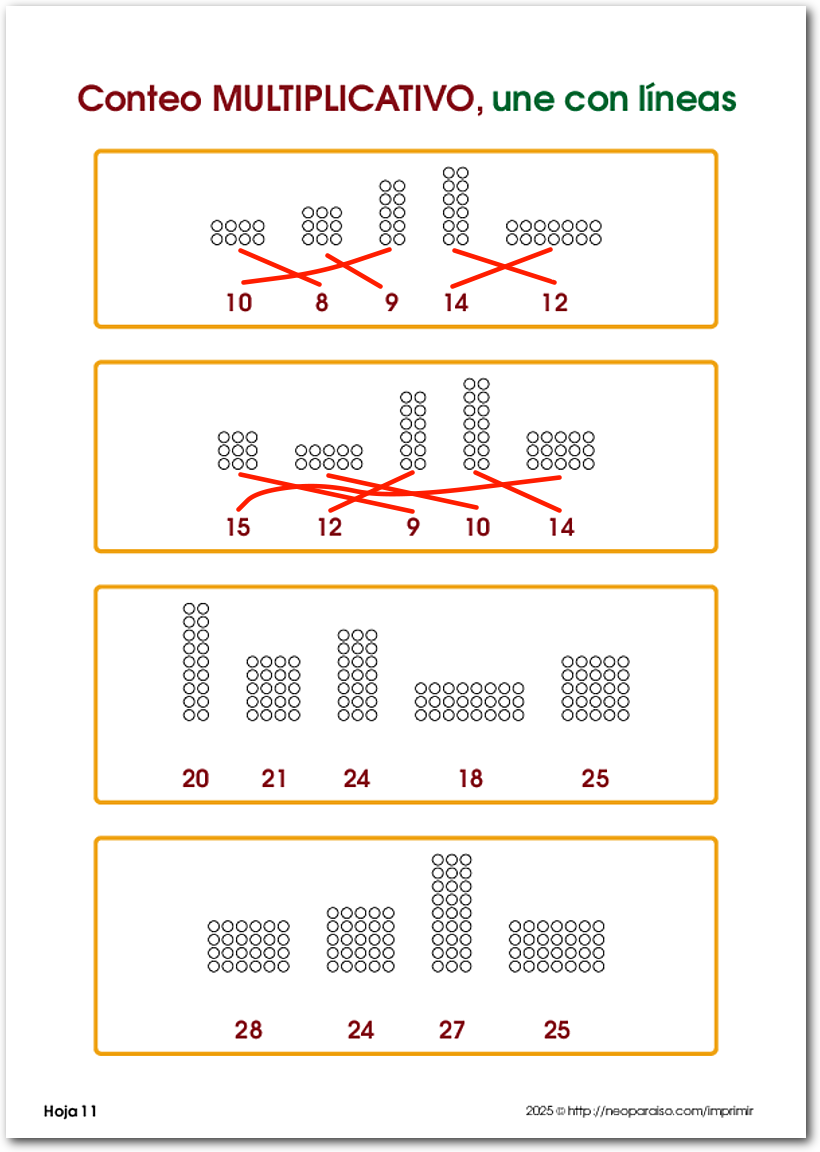
Conteo multiplicativo con bloques de círculos: una forma visual de entender la multiplicación
En el proceso de enseñanza de las matemáticas en los primeros grados de primaria, uno de los grandes retos es lograr que los niños comprendan lo que realmente significa multiplicar. Antes de aprender a recitar las tablas o resolver operaciones, es esencial que desarrollen una comprensión profunda y visual de lo que representa una multiplicación. Para apoyar este proceso, hemos creado una serie de hojas de trabajo que utilizan bloques de círculos organizados en filas y columnas para enseñar el conteo multiplicativo.
¿Cómo son estas hojas?
Cada hoja contiene varios bloques compuestos por círculos dispuestos en forma de rectángulos: filas y columnas claramente visibles. Por ejemplo, un bloque puede estar formado por 3 filas y 4 columnas de círculos, lo que representa un total de 12 círculos. La consigna para los niños es unir cada bloque con el número que representa la cantidad total de círculos que contiene. Así, el bloque mencionado debe conectarse con el número 12.
De lo visual a lo abstracto
Estos bloques rectangulares permiten que los niños visualicen la multiplicación como una suma repetida organizada:
- 3 filas de 4 círculos = 4 + 4 + 4 = 12,
- o 3 × 4 = 12.
Al ver los círculos distribuidos de manera regular, pueden contar fácilmente por filas o por columnas, y esto fortalece su comprensión de que la multiplicación no es solo una operación mecánica, sino una forma ordenada de contar grupos iguales.
Dificultad progresiva y autoevaluación
El nivel de dificultad de las hojas aumenta de arriba hacia abajo. Los primeros bloques contienen pocos círculos (por ejemplo, 2×2 o 3×2), mientras que los últimos pueden presentar configuraciones más complejas como 6×5 o 7×4.
Además, cada hoja está diseñada con un ingenioso mecanismo de auto-verificación. Las hojas impares y pares, aunque contienen diferentes bloques y números, están diseñadas para que el patrón de las líneas trazadas al unir correctamente cada bloque con su número coincida entre ambas. De este modo, los niños pueden revisar su propio trabajo comparando las hojas y confirmar visualmente si sus uniones son correctas.
¿Por qué usar estos bloques rectangulares?
Los bloques de círculos no solo hacen más atractiva y clara la actividad, sino que ayudan a los niños a:
- Internalizar el concepto de multiplicación como área (filas × columnas),
- Reforzar el conteo por grupos iguales (todas las filas de un bloque son iguales, todas las columnas de un bloque son iguales), lo que es la base del pensamiento multiplicativo,
- Desarrollar estrategias visuales y espaciales para resolver problemas matemáticos,
- Conectarse con conceptos posteriores como las tablas de multiplicar y el cálculo del área de figuras rectangulares.
Estas hojas son una herramienta poderosa para el aula o el trabajo en casa. Con ellas, los niños no solo practican la multiplicación, sino que la entienden, la ven y la viven a través de imágenes claras, ejercicios interactivos y mecanismos que fomentan la autonomía.
Si estás buscando recursos visuales y efectivos para introducir el conteo multiplicativo, ¡estas hojas pueden ser justo lo que necesitas!
Este es un recurso complementario a las láminas de conteo multiplicativo.