Rompecabezas de Orden de Operaciones
Utiliza la clave neoparaiso.com para abrir el PDF.
El orden de operaciones aritméticas es un concepto fundamental en matemáticas que los estudiantes deben dominar para resolver expresiones correctamente. Para facilitar este aprendizaje y hacerlo más atractivo, hemos diseñado unas hojas de trabajo innovadoras que combinan el desafío matemático con la satisfacción de resolver un rompecabezas.
1. ¿Cómo funciona este recurso?
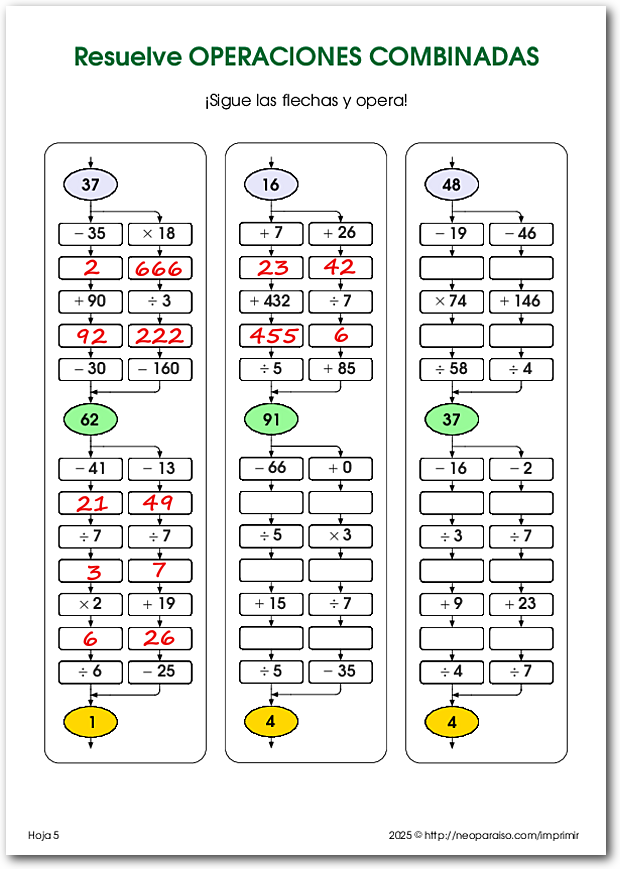
Cada hoja de trabajo presenta un conjunto de operaciones matemáticas de 4 números de 1 dígito, que los estudiantes deben resolver siguiendo el orden de operaciones correcto (PEMDAS: Paréntesis, Exponentes, Multiplicación y División, Suma y Resta). Junto a cada conjunto de operaciones hay un pequeño cuadrado que representa una pieza de un rompecabezas de 5x5. Cada cuadrado tiene sectores internos coloreados o en blanco.
Una vez que el estudiante resuelve la operación, debe buscar la respuesta en un rompecabezas vacío y ubicar la pieza correspondiente pintando su forma en el lugar adecuado. Al completar los 25 conjuntos de operaciones, el rompecabezas revelará un diseño hermoso, como un mandala, con simetría bilateral o rotacional. Esta característica permite a los estudiantes verificar visualmente si han colocado correctamente las piezas.
2. ¿Qué es PEMDAS y por qué es importante en matemáticas?
PEMDAS es una regla mnemotécnica que ayuda a recordar el orden correcto para resolver operaciones aritméticas. Su nombre proviene de las siglas en inglés de los pasos a seguir:
- P ↣ Paréntesis
- E ↣ Exponente (potenciación y raíces)
- MD ↣ Multiplicación y División (de izquierda a derecha)
- AS ↣ Adición y Sustracción (de izquierda a derecha)
Explicación paso a paso de Jerarquía de Operaciones.
- Paréntesis (P)
- Se resuelven primero todas las operaciones dentro de paréntesis () o corchetes []. Ejemplo:
- (3+5)×2 Primero resolvemos lo que está dentro del paréntesis:
- 8×2=16
- Exponente (E)
- Luego se calculan las potencias y raíces cuadradas. Ejemplo:
- 4+23 Primero resolvemos la potencia:
- 4+8=12
- Multiplicación y División (MD) - de izquierda a derecha. Se resuelven en el orden en que aparecen, de izquierda a derecha. Ejemplo:
- 10÷2×3 Primero hacemos la división:
- 5×3=15
- Adición y Sustracción (AS) - de izquierda a derecha. Finalmente, se realizan las sumas y restas en el orden en que aparecen. Ejemplo:
- 7+4-2 Primero sumamos:
- 11-2=9
3. Ejemplo completo aplicando PEMDAS
Supongamos la expresión: (2+3)×42÷2-5
- Paréntesis:
- 5×42÷2-5
- Exponente:
- 5×16÷2-5
- Multiplicación y División (de izquierda a derecha):
- 80÷2-5
- 40-5
- Suma y Resta:
- 35
4. ¿Cuándo se enseña el orden de operaciones?
El orden de operaciones se introduce en la educación primaria, generalmente entre 4to y 5to grado, con un enfoque inicial en paréntesis y operaciones básicas. En secundaria, alrededor de 6to y 7mo grado, se incorpora la potenciación, permitiendo a los estudiantes resolver problemas más complejos y sentar bases sólidas para el álgebra.
5. Mecanismos de auto-verificación incorporados
Para asegurar que los estudiantes puedan comprobar sus respuestas sin depender completamente del docente, estas hojas incluyen dos mecanismos de auto-verificación:
- Simetría en los diseños: Al completar el rompecabezas, la simetría en el diseño les permite notar errores si alguna pieza no encaja correctamente.
- Verificación entre pares: Las hojas de trabajo pares generan el mismo diseño que las hojas impares, permitiendo que los estudiantes comparen sus resultados con otro compañero y corroboren la exactitud de sus respuestas.
6. Formas de utilizar estas hojas en el aula
- Trabajo individual: Los estudiantes resuelven las operaciones y completan el rompecabezas de manera autónoma.
- Trabajo en parejas o grupos: Se asignan hojas pares e impares a diferentes estudiantes para que puedan comparar sus resultados.
- Desafíos matemáticos: Se puede realizar una competencia para ver quién completa el rompecabezas correctamente en el menor tiempo posible.
Este recurso convierte el aprendizaje matemático en una experiencia interactiva y entretenida. ¡Prueba estas hojas de trabajo en tu aula y descubre cómo los estudiantes pueden fortalecer sus habilidades matemáticas de una manera divertida y desafiante!