Tabla de Multiplicar del 1 al 100

Utiliza la clave neoparaiso.com para abrir el PDF.

Busco que los niños aprendan a registrar el producto de dos números en el cuadro de multiplicaciones. Aprendizaje Esperado: Que el niño resuelva problemas de multiplicación con números naturales.

La tabla de Multiplicar del 1 al 100, contiene en sus recuadros el resultado de multiplicar los números en negrilla de borde superior con los del borde izquierdo. Así, en la tabla se vé que 100 x 1 =100, 100 x 2 = 200, hasta 100 x 20 = 2000. Además están las tablas del 30 x 20 = 600, 40 x 20 = 800, o 50 x 20 = 1000, etc.

Puede leerse tanto vertical como horizontalmente. Al leerla horizontalmente nos da 20 números múltiplos de los números a la izquierda que van del 1 al 100. (Todo número distinto de 0 es múltiplo de sí mismo y de la unidad).

Al leerla verticalmente nos da 100 números múltiplos de los que están en la parte superior de la tabla. Los números en negrilla en la diagonal son los cuadrados de los números del 1 al 20. (1x1, 2x2, 3x3, etcetera). Esta también puede considerarse una tabla de multiplicación hasta el 100. Consta de dos páginas A4 y está en formato PDF.

Esta tabla de multiplicación también es conocida como tabla pitagórica y se utiliza en el aula para diferentes actividades como por ejemplo:

1. Usos de la Tabla Pitagórica

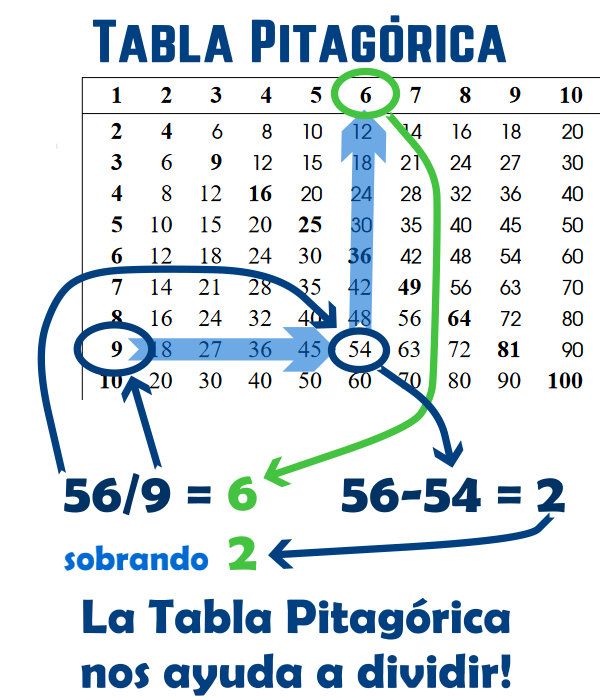
1.1. División con la Tabla Pitagórica

Para dividir con la Tabla Pitagórica buscas la fila de divisor (9) y luego recorres esa fila buscando el dividendo (56). Si lo encuentras bien! La división es exacta. Si no lo encuentras, determina el número inmediatamente menor que sí aparezca en la tabla (54) y sube por esa columna hasta encontrar el cociente (6).

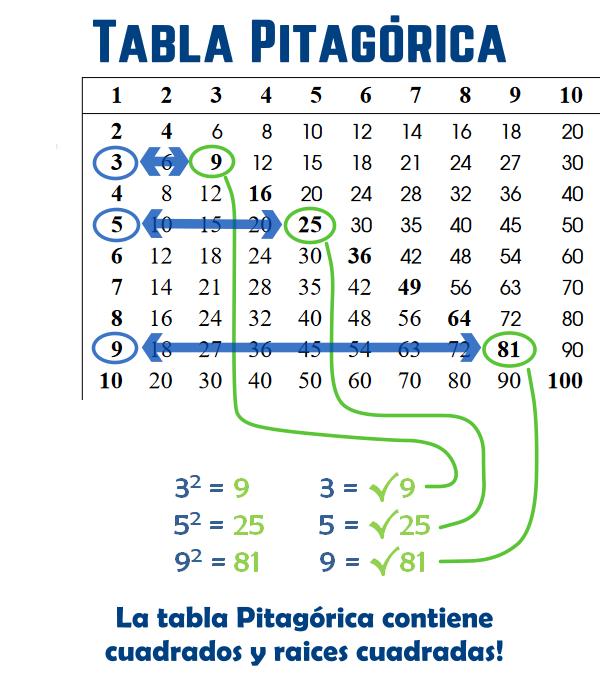
1.2. Números al cuadrado y Raices Cuadradas

Todos los números enteros de la tabla tienen sus cuadrados en la diagonal con números remarcados. De igual manera, de estos números de las diagonales se puede encontrar facilmente sus raices cuadradas al mirar los números de la extrama izquierda.

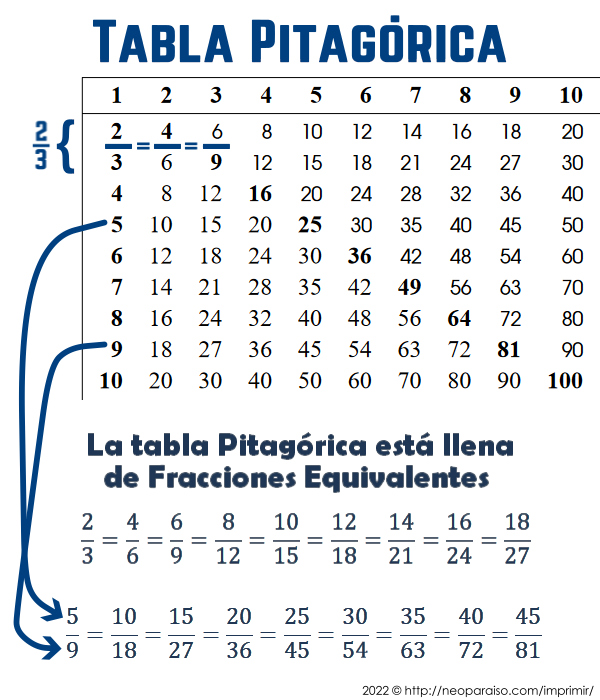
1.3. Fracciones Equivalentes en la Tabla Pitagórica

La Tabla Pitagórica está llena de fracciones equivalentes:

Funciona para 2 filas cualquiera, no solo para las filas adyacentes. Pueden doblar el papel y sacar las fracciones equivalentes de 5/9 por ejemplo. O pueden encontrar fracciones equivalentes para 5/8 mirando los múltiplos de 5 y los múltiplos de 8. Esto es más fácil si doblan la tabla (o corta las filas) y las coloca de manera que estas filas estén una sobre otra.

Funciona porque esencialmente estamos multiplicando el "numerador" y el "denominador" por el mismo valor. Si los números de la izquierda son 2 y 3 y pasamos a 6 y 9 (numerador/denominador) hemos multiplicado la fracción original por 1 (3/3). Este número 3 es el que está resaltado en el encabezado de la columna.

Lo que es CLAVE es que 3/3 es en realidad 1 y la propiedad de identidad significa que cuando multiplicamos un valor por 1, obtienemos el mismo número o "equivalente".

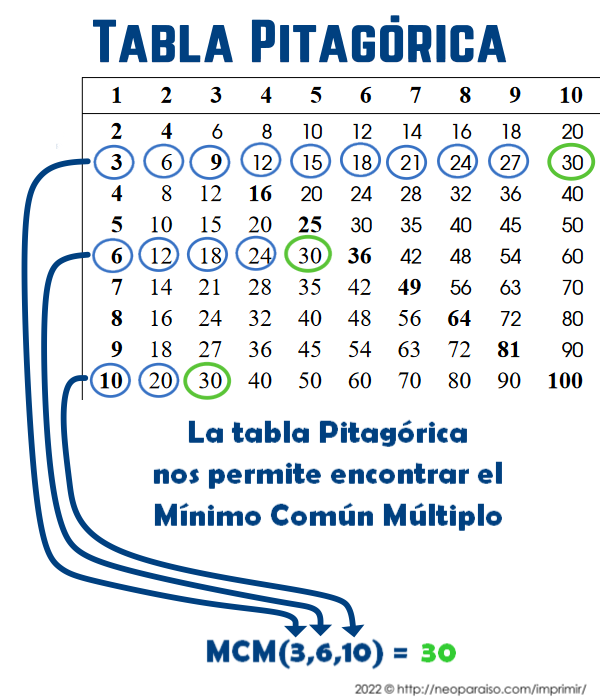
1.4. Mínimo Común Múltiplo con la Tabla Pitagórica

Plantee problemas de MCM (mínimo común múltiplo) y guíe a los estudiantes a encontrar múltiplos de los números del planteo de los problemas, luego guíelos a encontrar los múltiplos comunes, finalmente hágalos encontrar cual es el más pequeño de todos ellos (el mínimo de todos esos múltiplos) para resolver los problemas de MCM.

1.5. Es genial para la práctica las tablas

Una tabla o cuadrícula de multiplicación con espacios en blanco es una excelente manera de practicar tablas de multiplicar. Al completar la tabla, un niño practica cada multiplicación desde 1 x 1 hasta 10 x 10 (o 12 x 12 o más, ¡dependiendo de la tabla!).

Poder recordar las operaciones de multiplicación de manera rápida y precisa es muy importante para los niños cuando aprenden matemáticas. Las tablas de multiplicar surgen en muchas áreas de las matemáticas. Además, poder recordar fácilmente las operaciones de multiplicación también resulta útil en la vida cotidiana.

1.6. Es una herramienta de referencia útil

Un tabla de multiplicación es muy valiosa porque muestra todas las tablas de multiplicar claramente en una sola cuadrícula. Es una herramienta de referencia útil para los niños que necesitan aprender y memorizar sus multiplicaciones.

Una tabla pitagórica como ésta, también puede ser realmente útil en una situación en la que un niño necesita resolver multiplicaciones para practicar una habilidad matemática diferente.

Por ejemplo, a un niño que está trabajando en la búsqueda de áreas de rectángulos le resultaría difícil si no conocieran sus tablas de multiplicar (debe multiplicar el ancho por el largo para encontrar el área). Ser capaz de usar una tabla pitagórica como referencia significa que el niño todavía podrá tener éxito en encontrar el área del rectángulo, aunque todavía no pueda recordar las multiplicaciones con confianza.

2. Actividades con la Tabla Pitagórica

• Lo mejor de la multiplicación es que no importa el orden de los dos números que estás multiplicando. Por ejemplo, 9 x 6 es igual a 6 x 9. O 2 x 8 es igual a 8 x 2. Y esto también es cierto para la tabla de multiplicación, pida a los alumnos verificarlo en sus tablas.
• De hecho, si observa detenidamente, verá que la tabla se puede dividir en dos mitades mediante una línea diagonal marcada por los números en negrita.
• Los números en la parte inferior de la tabla se reflejan en la parte superior. Y si usa la parte superior para encontrar el producto de dos números o la parte inferior de la tabla, la respuesta será la misma.
• Haga que los estudiantes cuenten de 2 en 2, sombreando los múltiplos de 2 en amarillo en su tabla. Pídales que examinen los números cuidadosamente. Preguntar:
• ¿Qué patrones notan? (Los múltiplos de 2 son pares y siempre terminan en 0, 2, 4, 6 u 8.)
• Haga que los estudiantes cuenten de 5 en 5, rodeando los múltiplos de 5 con un marcador azul en sus tablas de números. Pedir:
• ¿Qué patrones notan? (Los múltiplos de 5 terminan en 5 o 0).
• Modele su pensamiento:
• Cuando miro los múltiplos de 2 y 5, veo que todos terminan en cero. Es como contar de 10 en 10. Noto que 2 x 5 es 10.
• Haga que los estudiantes cuenten 9 en 9 en la tabla de números. Escriba las multiplicaciones y las respuestas en la pizarra (9 x 1 = 9, 9 x 2 = 18, etc.) y pida a los alumnos que encuentren un patrón y discutan lo que encuentran.
• La suma de los dígitos del producto es 9.
• El dígito de las decenas es 1 menos que el otro factor (9 x 7 = 63, el 6 de 63 es 7-1.
• Estos patrones pueden ayudarlos a recordar y pueden usarse para verificar los productos.
• Haga que los estudiantes miren sus tablas y encuentren:
• los múltiplos que tienen en común 2 y 9 (18, 36, 54, 72, 90, etc.)
• los múltiplos que 2 y 5 tienen en común (10, 20, 30, 40, 50, etc.)
• los múltiplos que 5 y 9 tienen en común (45, 90)
• Pregunte a los alumnos qué pasaría si sombrearan todos los múltiplos de 1 en sus tablas. Pronto deberían darse cuenta de que estarían sombreando todo. Articular la propiedad de uno:
• El producto de un número y 1 es ese mismo número.
• Cada número es un múltiplo de 1 y en sí mismo.
• Para ilustrar, haga varias preguntas fáciles a la clase en general. ¿Cuánto es 8 x 1? ¿Qué es 9 x 1? Cada vez más difícil: ¿Qué es 52 x 1? ¿Qué es 1 millón x 1?)
• Pida a los alumnos que piensen en multiplicar con cero en términos de suma repetida. ¿Qué es 0 + 0? ¿Qué es 3 x 0? ¿Qué es 52 x 0? ¿Qué es 1 millón x 0? Ayude a los estudiantes a determinar la propiedad cero para la multiplicación:
• El producto de un número y 0 es 0.
• Otros patrones a detectar:
• Los múltiplos de 8 eran el doble de los múltiplos de 4
• Los múltiplos de 9 se suman para ser igual a 9 o un múltiplo de 9
• Algunos de los múltiplos de 5 también son múltiplos de 10 porque 5 es un factor de 10
• Los números pares se repiten en el lugar de las unidades, pero los números impares no. (Ejemplo: para los múltiplos de 4, el lugar de las unidades termina con 4, 8, 2, 6 y 0 repetidamente).
• Pida a los alumnos que nombren el doble de 2 (2 x 2 = 4). Comparta el siguiente problema:
• Para su reunión familiar, Ariel quiere hacer 2 pasteles de limón que usan 5 limones cada uno. ¿Cuántos limones debería comprar? (2 x 5 = 10). Luego recuerda que su tío Bob ama los limones y es probable que coma 2 pasteles él solo. Ariel mejor quiere hacer 4 pasteles! ¿Cuántos limones necesitará para hacer 4 pasteles que requieren 5 limones cada uno?
• Explique a los alumnos que pueden llegar a la respuesta a través de la idea del doble. Ejemplo:
• 2 x 5 = 10
• 4 x 5 = 10 + 10
• 4 x 5 = 20
• Como 4 es el doble de 2, el producto de cualquier número multiplicado por 4 será el doble del producto de ese mismo número multiplicado por 2.
• Pida a los alumnos que nombren otros dobles con los que podría funcionar esta técnica, como
• 4 x 2 = 8 y 4 x 6 = 24.
• 4 x 6 = 24
• 8 x 6 = 24 + 24
• 4 x 2 = 8 y 4 x 7 = 28.
• 4 x 7 = 28
• 8 x 7 = 28 + 28
• 4 x 2 = 8 y 4 x 8 = 32
• 4 x 8 = 32
• 8 x 8 = 32 + 32
• Veamos los números al cuadrado. El cuadrado de un número es el producto de un número multiplicado por sí mismo. Por ejemplo, 25 es un número cuadrado porque es igual a 5 x 5. En la tabla, los números cuadrados forman una línea diagonal recta en negrita.

LO MÁS DESCARGADO

Otros también vieron:

Multiplicación

Tabla

Varias Cifras

Síguenos en Facebook